5. Übungen
1. Licht und Strahlung
Elektromagnetische Wellen (2/4)
Aufgabe: Laufzeit des Sonnenlichts und Mondlichts bis zur Erde
a) Der Abstand der Erde von der Sonne ist etwa 150·106 km. Wie viel Zeit (in Sekunden und in Minuten) dauert es, bis das von der Sonne ausgesandte Licht die Erde erreicht?
b) Der Mond ist von der Erde 384 000 km entfernt, also viel näher als die Sonne. Wie viel Zeit verstreicht, bis das vom Mond reflektierte Sonnenlicht die Erde erreicht?
Lösungen:
a) Die Zeit von der Sonne zur Erde beträgt
oder 8,33 Minuten.
b) Für die Zeit vom Mond zur Erde gilt
Aufgabe: Das Lichtjahr und die Entfernung zu Alpha Centauri
Der sonnennächste Stern hat den Namen Alpha Centauri. Seine Entfernung wird mit 4,247 Lichtjahren angegeben. Ein Lichtjahr ist die Strecke, welche das Licht in einem Jahr zurücklegt, eine in der Astronomie sehr oft genutzte Längeneinheit. Wie vielen Kilometern entspricht ein Lichtjahr? Wie weit in Kilometern ist Alpha Centauri entfernt? Sie werden feststellen, dass Lichtjahre eine sehr praktische Längeneinheit sind, um Entfernungsangaben zu fernen Himmelskörpern nicht zu unhandlich werden zu lassen!
Lösung:
Ein Lichtjahr entspricht dem Produkt aus Lichtgeschwindigkeit und der Zeit 1 Jahr, d.h. der Zeit 365 Tage mit jeweils 24 Stunden, 60 Minuten und 60 Sekunden, d.h. aus 31,536·106 Sekunden.
oder 9,461·1012 km oder ca. 9,5 Billionen Kilometer. Die Distanz 4,247 Lichtjahre zu Alpha Centauri entspricht ca. 40 Billionen Kilometer.
Elektromagnetische Wellen (4/4)
Arbeitsblatt 1.1: Licht und Strahlung
Bitte prüfen und vertiefen Sie Ihre Kenntnisse zum Thema dieses Kapitels mit dem Arbeitsblatt 1.1: Licht und Strahlung. Es kann auch als Präsenz- oder Hausaufgabe im Unterricht verwendet werden.
Photonen (4/4)
Aufgabe: Ein Blitz aus 1000 Photonen
In dunkler Nacht sehen wir weit entfernt das Blitzlicht eines Fotoapparats aufblitzen. Wir nehmen an, durch die Pupille unseres Auges treten 1000 Photonen des Blitzes auf die Netzhaut, ein wirklich sehr schwacher Lichtblitz. In der linken Spalte unten steht, dass ein dunkeladaptiertes Auge diesen Blitz wohl gerade noch schwach wahrnehmen kann.
Der Durchmesser der Pupille sei 4 mm. Die Lichtwellenlänge sei 500 nm (tatsächlich ist ein Blitzlicht weiß). Die Blitzdauer ist 1 ms, dies entspricht der Leuchtdauer von Fotoblitzen.
a) Berechnen Sie die Energie eines einzelnen Photons in Elektronenvolt und des aus 1000 Photonen bestehenden Blitzes in Joule.
b) Die Photonen seien gleichmäßig über die Blitzdauer verteilt. Welche momentane Leistung tritt durch die Pupille?
c) Welche Bestrahlungsstärke in W/m2 zeigt der Blitz an unserem Standort?
Lösungen:
a) Die Energie eines Photons ist:
1 J entspricht 1,6·10-19 eV. Es wird: E = 2,48 eV. Vergleichen Sie das Ergebnis mit der Grafik auf der Seite Photonen (3/4).
Die Gesamtenergie der 1000 Photonen des Blitzes im Auge ist 0,4·10-15 J oder 0,4 fJ. (10-15 = 1 Billiardstel = 1 Femto, Kurzzeichen f)
b) Die Blitzenergie tritt in einer Millisekunde auf. Die Leistung durch die Pupille während der Blitzdauer wird:
oder 0,4 pW. (10-12 = 1 Billionstel = 1 Piko, Kurzzeichen p)
Kaum zu glauben, dass das Auge solche Blitze sehen kann!
c) Der Radius der Pupille is r = 2 mm. Die hindurch tretende Leistung ist 0,4·10-12 W. Die Bestrahlungsstärke wird damit:
oder 32 nW/m2. Zum Vergleich: Bei wolkenlosem Himmel ist die Bestrahlungsstärke am Boden bei Vollmond etwa 3 mW/m2, die Sonne im Zenit strahlt mit etwa 1 kW/m2.
Spektralanalyse: Farbglasfilter (4/4)
Aufgabe: Reflektanzen
Betrachten Sie vergleichend die Schwarz-Weiß-Aufnahmen der Bänder 1 bis 4 und die Falschfarbenaufnahme.- Beurteilen Sie bitte die Reflektanzen vegetationsreicher und vegetationsarmer Landoberflächen und des Meerwassers anhand der jeweiligen Helligkeit.
- Auf der vorherigen Seite findet sich die Tabelle der TM-Bänder. Lassen sich die in der Spalte Bedeutung genannten Möglichkeiten bestätigen?
- Prüfen Sie Ihre Befunde durch Vergleich mit Informationen in weiterführenden SEOS-Seiten
- zu den spektroskopischen Eigenschaften von Vegetation in der Lerneinheit Fernerkundung in der Landwirtschaft
- zu den spektroskopischen Eigenschaften von Meerwasser in der Lerneinheit Meeresfarben in Küstengewässern
- zur Klassifizierung von Satellitenbildern in der Lerneinheit Algorithmen und Methoden der Klassifizierung
Bei dieser Aufgabe werden keine Antworten vorgeschlagen.
Zu Ergänzung 1.1: Die Maxwell-Gleichungen
Aufgabe 1: Divergenz und Rotation eines Vektors
Bitte zeigen Sie, dass die Gleichungen für die Divergenz und die Rotation des elektrischen Feldvektors richtig sind. Sind diese Terme skalare Größen oder Vektoren?
Lösungen:
ist ein Skalar,
ist ein Vektor. Die Größen , und sind die Einheitsvektoren in Richtung der -, - und -Koordinaten.
Aufgabe 2: Gradient eines Skalars
Der Vollständigkeit wegen sei erwähnt, dass der ∇-Operator auch auf skalare Größen angewandt werden kann. Sei eine skalare Funktion im Raum, z.B. das elektrische Potenzial. Der Ausdruck ∇φ bezeichnet dann die räumliche Ableitung von φ, was auch als grad φ geschrieben werden kann. ∇φ ist ein Vektor, da der Vektor ∇ mit dem Skalar φ multipliziert wird.
Bitte schreiben Sie ∇φ komponentenweise in Richtung x, y, und z.
Lösung:
Zu Ergänzung 1.2:
Maxwell-Gleichungen und elektromagnetische Wellen
Aufgabe 1: Der Laplace-Operator
Der Nabla-Operator, in kartesischen Koordinaten geschrieben,
entspricht der ersten räumlichen Ableitung. Das Skalarprodukt ist dann die zweite räumliche Ableitung, der Laplace-Operator.
a) Bitte zeigen Sie, dass für den Laplace-Operator in kartesischen Koordinaten gilt:
b) Bitte schreiben Sie die Wellengleichung des elektrischen Felds in Komponenten für kartesische Koordinaten.
Lösung:
a)
b) Für das elektrische Feld einer Welle in beliebiger Richtung wird die x-Komponente:
und entsprechend für die y- und z-Komponenten sowie die Komponenten des Magnetfelds.
Aufgabe 2: Die dritte Maxwell-Gleichung in kartesischen Koordinaten
Bitte zeigen Sie durch eine Rechnung, dass die Feldvektoren
angewandt auf die dritte Maxwell-Gleichung, die folgenden Komponentengleichungen liefern:
Lösung:
Die dritte Maxwell-Gleichung
In Komponenten:
Hieraus folgt die Behauptung.
Zu Ergänzung 1.4:
Energiedichte und Bestrahlungsstärke elektromagnetischer Wellen
Aufgabe 1: Elektrisches und magnetisches Feld der Sonnenstrahlung
In Kapitel 2 Temperaturstrahlung wird gezeigt: die Bestrahlungsstärke der Sonnenstrahlung am Außenrand der Erdatmmosphäre hat den Wert 1361 W/m², was als Solarkonstante bezeichnet wird. Berechnen Sie bitte die elektrische und die magnetische Feldstärke dieser Strahlung.
Lösung:
Mit , und folgt:
Das elektrische Feld ist sehr stark, das magnetsche Feld recht klein. Die Ursache ist - wie in der Ergänzung gezeigt - der Zusammenhang . Allerdings sind die Feldenergien des elektrischen und des magnetischen Felds gleich groß.
Es wird hier die Amplitude einer ebenen monochromatischen Welle berechnet, was für die Sonnenstrahlung mit ihrem breiten Spektrum nicht zutrifft. Die Zahlenwerte des Ergebnisses sind trotzdem gültig, da spektrale Eigenschaften in die Berechnung der Feldstärken nicht eingehen.
Zu Ergänzung 1.6: Der Strahlungsdruck
Aufgabe 1: Der Strahlungsdruck der Sonnenstrahlung
-
In Kapitel 3, Abschnitt Klima und
Klimawandel, wird gezeigt: die Bestrahlungsstärke der Sonnenstrahlung am
Außenrand der Erdatmosphäre hat den Wert 1361 W/m²; dies ist die
sogenannte Solarkonstante. Wie groß ist der Strahlungsdruck der Sonnenstrahlung?
Lösung:
Es gilt:
Mit und erhält man: -
Reduziert durch Absorption und Streuung an den Luftmolekülen kommen an einem wolkenfreien
Tag etwa 65% der am Außenrand der Atmosphäre vorhandenen Sonnenstrahlung an der
Erdoberfläche an. Vergleichen Sie den hier vorhandenen Strahlungsdruck mit dem Luftdruck
auf Meeresniveau, der gemittelt 1013 hPa beträgt.
Lösung:
65% des Strahlungsdrucks am Außenrand der Atmosphäre ergibt an der Erdoberfläche. 1013 hPa Standardluftdruck ist in Relation zu diesem Strahlungsdruck 34·109 mal größer. Der Strahlungsdruck spielt für mechanische Vorgänge an der Erdoberfläche daher keine Rolle. -
Ebenfalls in Kapitel 3, Abschnitt
Klima und Klimawandel, wird die spezifische Ausstrahlung der Photosphäre der Sonne
berechnet. Die Photosphäre ist der Bereich der Sonnenatmosphäre, in dem die in den
Weltraum gerichtete Sonnenstrahlung entsteht. Sie beträgt 62,9 MW/m². Welchen Wert
hat dort der Strahlungsdruck?
Lösung:
Die entsprechende Rechnung ergibt . Der Gasdruck der Photosphäre der Sonne beträgt 0,87 hPa an ihrem oberen bzw. 125 hPa am unteren Rand. Auch hier spielt der Strahlungsdruck nur eine geringe Rolle. -
Weltraumagenturen untersuchen, wie der Strahlungsdruck für den Antrieb von Raumfahrzeugen
genutzt werden kann. Die mit einem Sonnensegel erreichbare Beschleunigung ist
für bemannte Raumflüge zwar zu gering, soll aber langjährig angelegte
Missionen kleiner unbemannter Satelliten ohne zusätzlichen Antrieb möglich
machen.
Eine Herausforderung ist es, Materialien für leichte und gleichzeitig robuste Segel und die mechanischen Strukturen für ihre Entfaltung im Weltraum zu entwickeln. Der neueste Versuch der NASA (letzter Aufruf: 16.04.2025) hat zum Ziel, eine Sonde mit 16 kg Gesamtmasse mit einem 80 m² großen Segel anzutreiben. Die Erdumlaufbahn soll sonnensynchron sein, sodass die Sonne jederzeit das Segel senkrecht mit der Solarkonstante 1361 W/m² beleuchtet. Berechnen Sie bitte die damit erreichbare Beschleunigung.
Lösung:
Es ist
mit der Segelfläche und einem ideal reflektierenden Segel mit dem Reflexionskoeffizienten , und mit der Masse des Satelliten. Die Beschleunigung ergibt sich zu,ein eher kleiner Wert. Immerhin hat sich die Geschwindigkeit nach einem Tag (nach 86400 Sekunden) um 6,27 m/s geändert.
Arbeitsblatt 1.2: Kometenschweife
Bitte ergänzen Sie Ihre Kenntnisse zum Thema Strahlungsdruck mit dem Arbeitsblatt 1.2: Kometenschweife.
Aufgaben: Kometenschweife
-
Berechnen Sie das Verhältnis von Schwerkraft und Kraft durch den Strahlungsdruck.
Wie ist die Abhängigkeit des Quotienten von der Dichte, dem Durchmesser und dem
Abstand zur Sonne?
Lösung:
Das Verhältnis ist proportional zur Dichte und Teilchengröße. Der Abstand zur Sonne ist nicht von Bedeutung. -
Kleine Eiskristalle im Kometenschweif haben die Dichte des Wassers, also ca. 1000
kg/m3. Für welchen Teilchendurchmesser heben sich die Kraft des
Strahlungsdrucks und die Schwerkraft auf? Ist die Hypothese richtig, kleine Teilchen
würden durch den Strahlungsdruck abgestoßen und große Teilchen in Richtung der Sonne
angezogen?
Lösung:
fürDie Hypothese ist richtig. Die kritische Größe absorbierender Teilchen, bei der beide Kräfte gleich sind, ist etwa 1 µm. -
Die Teilchen in Kometenschweifen sind offensichtlich eher reflektierend statt
absorbierend. Wie ändert sich der Durchmesser, bei dem die beiden Kräfte gleich
groß sind, für ideal reflektierende Teilchen?
Lösung:
Die Kraft durch den Strahlungsdruck auf ideal reflektierende Teilchen verdoppelt sich, die Schwerkraft bleibt gleich. Daher halbiert sich die kritische Teilchengröße.
Zu Ergänzung 1.7: Strahlungsgrößen und Radiometrie
Aufgabe 1: Die Strahlstärke der Sonne
Die gesamte Strahlungsleistung der Sonne ist 387,5·1024 W. Die Strahlung sei isotrop in den Raum gerichtet. Der Abstand der Sonne zur Erde ist 149 589 000 km (die sog. Astronomische Einheit, AU). Wegen dieser großen Entfernung können wir von der Erde aus die Sonne näherungsweise als Punktlichtquelle ansehen. Der Radius der Erde ist 6371 km.
-
Welchen Wert hat die Strahlstärke der Sonne in den gesamten Weltraum? Welche Strahlstärke trifft die Erde
insgesamt bzw. einen Quadratmeter der Erde?
Lösung:
Die Strahlstärke der Sonnenoberfläche ist:
Für einen isotropen Strahler ist die Strahlstärke konstant, die Strahlungsleistung ändert sich also proportional zum Raumwinkel. Die Strahlstärke, welche die Erde als Ganzes trifft, und die Strahlstärke für einen Quadratmeter der Erde haben daher den gleichen Wert wie die Strahlstärke der Sonne in den Weltraum.
-
Berechnen Sie den Raumwinkel, unter dem die Erde von der Sonne aus erscheint.
Wie groß ist die auf die Erde treffende Strahlungsleistung?
Lösung:
Mit den Daten für den Erdradius und den Abstand der Erde von der Sonne folgt für den Raumwinkel , unter dem die Querschnittsfläche der Erde von der Sonne aus erscheint:
Wegen der Isotropie der Sonnenstrahlung gilt:
Für die Strahlungsleistung , welche auf den Querschnitt der Erde trifft, folgt:
-
Berechnen Sie den Raumwinkel, unter dem ein Quadratmeter der Erde von der Sonne aus erscheint,
sowie die auf einen Quadratmeter der Erde fallende Strahlungsleistung. Vergleichen Sie das Ergebnis mit der
in Kapitel 3 angegebenen Solarkonstante, welche
der Bestrahlungsstärke am Außenrand der Erdatmosphäre entspricht.
Lösung:
Der Raumwinkel für einen Quadratmeter der Erdoberfläche ist:
Es gilt wieder:
Die Strahlungsleistung wird:
Die Solarkonstante ist 1361 W/m². Innerhalb der Genauigkeit dieser Abschätzung ist die Übereinstimmung recht gut.
Aufgabe 2: Isotrope Strahler
-
Vergrößern Sie den Raumwinkel des in Richtung Zenit orientierten Kegels zu einer Halbkugel (oder:
zu einem Halbraum). Wie ist dann der Zusammenhang zwischen Strahlungsleistung und Strahlstärke?
Lösung:
Bei einem kegelförmigen Raumwinkel, in Richtung Zenit orientiert, variiert der Azimutwinkel von 0 bis . Der Zenitwinkel variiert von 0 bis zum halben Öffnungswinkel :
Für wird .
-
Vergrößern Sie den Raumwinkel weiter bis zum ganzen Raum und berechnen Sie wieder den Zusammenhang.
Lösung:
Für wird . Dieses Ergebnis war schon am Anfang des Abschnitts über die Strahlstärke gefunden worden.
Aufgabe 3: Anisotrope Strahler
Die axialsymmetrische Strahlstärke einer Lampe sei durch
-
Skizzieren Sie bitte die Verteilung der Strahlstärke über den Zenitwinkel ϑ von 0 bis 180°.
Lösung:
 Strahlstärke des anisotropen Strahlers in Abhängigkeit des Zenitwinkels ϑ.
Strahlstärke des anisotropen Strahlers in Abhängigkeit des Zenitwinkels ϑ. -
Berechnen Sie die insgesamt emittierte Strahlungsleistung als Funktion der Strahlstärke für ϑ = 0.
Antwort:
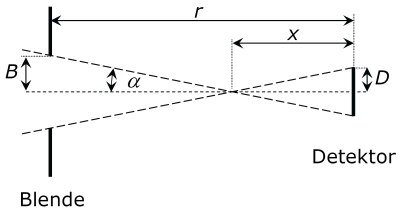
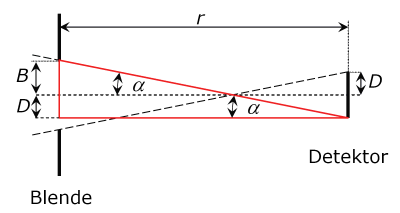
Aufgabe 4: Gesichtsfeld eines Detektors mit Blende
Detektor und Blende sind im Abstand r angeordnet. Der Radius des Detektors ist D, der Radius der Blende ist B. ist der größtmögliche halbe Gesichtsfeldwinkel.
Bestimmen Sie bitte aus den geometrischen Verhältnissen eine Gleichung für den Gesichtsfeldwinkel in Abhängigkeit von B und D.
Hinweis: Finden Sie ein rechtwinkliges Dreieck, das den Winkel sowie die Radien B und D enthält.
Lösung:Aufgabe 5: Gesichtsfeld eines Detektors mit Linse und Blende
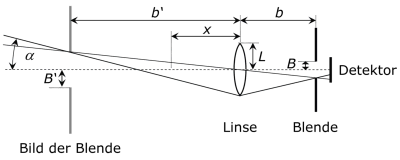
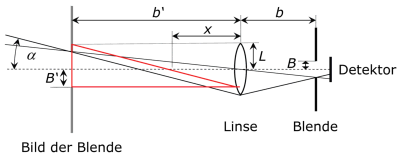
Die Signalausbeute eines Detektors mit Blende ist sehr gering. Viel bessere Lichtausbeuten erhält man, wenn die Anordnung mit einer Linse ergänzt wird.
Der maximale Empfangswinkel wird durch die Linse (mit Radius L und Brennweite f) und die Blende im Abstand b festgelegt. Die empfindliche Fläche des Detektors hinter der Blende sei so groß gewählt, dass sie den Strahlengang nicht begrenzt. Der größtmögliche halbe Gesichtsfeldwinkel ergibt sich aus dem Bild der Blende B' im Abstand b' von der Linse.
a) Bestimmen Sie bitte aus den geometrischen Verhältnissen und mit den Abbildungsgleichungen für eine Linse eine Beziehung für den Gesichtsfeldwinkel in Abhängigkeit von L, B, b und f.
Hinweis: Finden Sie wieder ein rechtwinkliges Dreieck, das nun den Winkel sowie die Größen L, B' und b' enthält. Nutzen Sie die Linsenabbildungsgleichungen, um aus B' und b' die Beziehung als Funktion von B und b darzustellen.
b) Wie vereinfacht sich das Ergebnis für b=f, d.h. wenn die Blende im Abstand der Brennweite der Linse steht?
Lösung:a)
b)
Zu Ergänzung 1.8: Lambert-Strahler, Kosinus-Strahler
Aufgabe 1: Die Strahlungsleistung von Kosinus-Strahlern
Eine wichtige Gruppe anisotroper axialsymmetrischer Strahler sind die Kosinus-Strahler. Ihre Strahlstärke nimmt mit zunehmendem Zenitwinkel ϑ im Bereich von 0 bis entsprechend cos ϑ ab:
Berechnen Sie bitte die Strahlungsleistung in einen kegelförmigen Raumwinkel mit dem maximalen Zenitwinkel
ϑ' sowie die Strahlungsleistung in den oberen Halbraum.
Lösung:
Die Strahlungsleistung in den oberen Halbraum: