5. Übungen

2. Temperaturstrahlung

Zu Ergänzung 2.1: Absorption, Emission und Reflexion

Aufgabe: Vom Ungleichgewicht zum Gleichgewicht

Zwei Körper im thermischen Gleichgewicht in einem von der Umgebung isolierten Hohlraum. Die Pfeile stellen die jeweiligen Strahlungsflüsse dar. Die Buchstaben r, e und a in den kurzen Pfeilen stehen für reflektiert, emittiert und absorbiert.

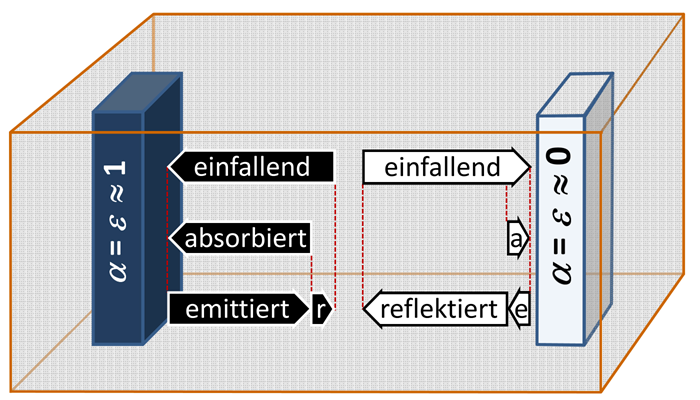
Skizzieren Sie wie in der Grafik, wie sich die Länge der Pfeile für folgende Fälle ändert:

der schwarze Körper hat eine höhere Temperatur als der weiße
der weiße Körper hat eine höhere Temperatur als der schwarze.

Fragen:

wie ändern sich die Längen der Pfeile für die absorbierte und emittierte Strahlung beider Körper?
welche Pfeillängen ergeben sich jeweils für die einfallende und die reflektierte Strahlung?
erklären Sie, wie in der Tendenz eine Angleichung der Temperaturen zustande kommt.

Lösung:

Die Verhältnisse sind etwas verwickelt und auf den ersten Blick unübersichtlich. Für das Verständnis sind Skizzen der Strahlungsbilanzen sehr hilfreich. Die folgenden Hinweise sollen hierbei eine Hilfestellung sein. Die Angaben beziehen sich auf den Anfangszustands des Kontakts zweier Körper, von denen einer eine höhere Temperatur besitzt und der andere die Temperatur des vorherigen Gleichgewichts aufweist.

a) der schwarze Körper hat eine höhere Temperatur als der weiße.

Zu 1: Schwarzer Körper: emittiert und absorbiert sind größer. Weißer Körper: emittiert bleibt gleich, absorbiert ist größer.
Zu 2: Schwarzer Körper: einfallend und reflektiert sind größer. Weißer Körper: einfallend und reflektiert sind größer.
Zu 3: die Emission des weißen Körpers bleibt gleich, alle anderen Größen wachsen; die Bilanz ist für den weißen Körper höher als für den schwarzen.

b) der weiße Körper hat eine höhere Temperatur als der schwarze.

Zu 1: Schwarzer Körper: emittiert bleibt gleich, absorbiert ist größer. Weißer Körper: emittiert und absorbiert sind größer.
Zu 2: Schwarzer Körper: einfallend und reflektiert sind größer. Weißer Körper: einfallend und reflektiert sind größer.
Zu 3: die Emission des weißen Körpers bleibt gleich, alle anderen Größen wachsen; die Bilanz ist für den schwarzen Körper höher als für den weißen.

Zu Ergänzung 2.6: Differenziale und Ableitungen

Aufgabe 1: partielle Ableitung und Differenzial

Bestimmen Sie bitte die partiellen Ableitungen und das totale Differenzial von:

z = x^{3} y + x^{2} y^{2} + x y^{3}

z = x sin y - y sin x

Lösungen:

z = x^{3} y + x^{2} y^{2} + x y^{3}

Die partiellen Ableitungen:

\frac{\partial z}{\partial x} = 3 x^{2} y + 2 x y^{2} + y^{3}

\frac{\partial z}{\partial y} = x^{3} + 2 x^{2} y + 3 x y^{2}

Das Differenzial:

d z = (3 x^{2} y + 2 x y^{2} + y^{3}) d x + (x^{3} + 2 x^{2} y + 3 x y^{2}) d y

z = x sin y - y sin x

Die partiellen Ableitungen:

\frac{\partial z}{\partial x} = sin y - y cos x

\frac{\partial z}{\partial y} = x cos y - sin x

Das Differenzial:

d z = (sin y - y cos x) d x + (x cos y - sin x) d y

Aufgabe 2: totales Differenzial

Bestimmen Sie die totale Ableitung von

z = x^{2} + 3 x y + 5 y^{2}

mit $x = sin t$ und $y = cos t$ .

Lösung:

Die partiellen Ableitungen:

\frac{\partial z}{\partial x} = 2 x + 3 y

\frac{\partial z}{\partial y} = 3 x + 10 y

Die Ableitungen der Variablen:

\frac{d x}{d t} = cos t

\frac{d y}{d t} = - sin t

Das totale Differenzial:

\frac{d z}{d t} = (2 sin t + 3 cos t) cos t - (3 sin t + 10 cos t) sin t

Aufgabe 3: partielle Ableitung und totales Differenzial eines Vektors

Die Rechenregel für das Differenzial gilt nicht nur für Skalare, sondern in gleicher Weise auch für Vektoren. Wir betrachten den Vektor $\vec{A} (x, y, z)$ :

d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z

Berechnen Sie bitte die partiellen Ableitungen und das totales Differenzial von

\vec{A} = (x^{2} sin y, z^{2} cos y, - x y^{2})

Lösung:

Ausgehend von der Definition des totalen Differenzials:

\begin{array}{l} d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z \\ = (2 x sin y,0, - y^{2}) d x + (x^{2} cos y, - z^{2} sin y, - 2 x y) d y \\ + (0,2 z cos y,0) d z \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{array}

Alternativ kann man auch unmittelbar das totale Differential jedes Einzelterms von $\vec{A}$ bilden:

\begin{matrix} d \vec{A} = (d (x^{2} sin y), d (z^{2} cos y), d (- x y^{2})) \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{matrix}

Aufgabe 4: Temperatur in Raum und Zeit

Die Temperatur sei durch die folgende Funktion gegeben:

T = T_{o} + a x - b x y^{2} + c y z^{2} + d z t

mit:
$T_{o}$ =20°C
$a$ =0,3°C/m
$b$ =0,02°C/m³
$c$ =0,1°C/m³
$d$ =0,01°C/(m·s)

a) Wie ist die Temperatur am Ort $\vec{r}' = (x', y', z')$ = (10 m, 5 m, 2 m) zur Zeit $t'$ = 100 s.

b) Berechnen Sie die partiellen Ableitungen der Temperatur. Welche Werte haben sie am Ort $\vec{r}'$ zur Zeit $t'$ ?

c) Berechnen Sie die Temperaturänderung $d T$ für eine Verschiebung $d \vec{r} = (d x, d y, d z)$ = (1 m, 0,5 m, 0,5 m) um eine Zeit $d t$ = 2 s später.
(Wir behandeln die Differenziale näherungsweise als endliche Größen)

d) Welchen Wert hat die Temperatur $T (\vec{r}' + d \vec{r}, t' + d t)$ ?

Lösung:

a) $T (\vec{r}', t')$ = 22°C

b)	$\frac{\partial T}{\partial x} = a - b y$	${(\frac{\partial T}{\partial x})}_{\vec{r}', t'}$ = 0,2°C/m
	$\frac{\partial T}{\partial y} = - 2 b x y + c z^{2}$	${(\frac{\partial T}{\partial y})}_{\vec{r}', t'}$ = 0,4°C/m
	$\frac{\partial T}{\partial z} = 2 c y z + d t$	${(\frac{\partial T}{\partial z})}_{\vec{r}', t'}$ = 3°C/m
	$\frac{\partial T}{\partial t} = d z$	${(\frac{\partial T}{\partial t})}_{\vec{r}', t'}$ = 0,02°C/m

c) $d T$ = 1,94°C

d) $T (\vec{r}' + d \vec{r}, t' + d t)$ = 21,94°C

Aufgabe 4: Nabla-Operator und Geschwindigkeitsvektor

Der Nabla-Operator lässt sich mit einem Vektor, zum Beispiel mit der Geschwindigkeit, verknüpfen.

a) Stellen Sie die Ausdrücke $\nabla \cdot \vec{v}$ und $\nabla \times \vec{v}$ ` in kartesischen Koordinaten dar. Sind sie Skalare oder Vektoren?

b) Welche Bedeutung haben diese Ausdrücke? Was bedeutet der Ausdruck $\vec{v} \cdot \nabla$ ?

Lösung:

\nabla \cdot \vec{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}

\nabla \times \vec{v} = | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & v & w \end{matrix} | = ((\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z}), (\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}), (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}))

mit den Einheitsvektoren $\vec{i}$ , $\vec{j}$ und $\vec{k}$ in Richtung der Koordinatenachsen $x$ , $y$ und $z$ .

$\nabla \cdot \vec{v}$ ist ein Skalar, $\nabla \times \vec{v}$ ist ein Vektor.

Der Ausdruck $\nabla \cdot \vec{v}$ wird auch als Divergenz der Geschwindigkeit bezeichnet und kennzeichnet ihre Quellen oder Senken. Ist seine Bilanz in einem Gebiet positiv, so liegt in dem Gebiet eine Quelle für Geschwindigkeit vor, wie es etwa bei einem expandierenden Gas der Fall ist. Ist die Bilanz in einem Gebiet negativ, so wird das Gas komprimiert. Weiterführendes Stichwort: Gaußscher Satz.

Der Ausdruck $\nabla \times \vec{v}$ wird auch als Rotation der Geschwindigkeit bezeichnet und kennzeichnet die Wirbelstärke der Geschwindigkeit. Sie ist ungleich Null bei Vorliegen von Scherungen in der Strömung, sowie bei Wirbeln oder Turbulenzen. Weiterführendes Stichwort: Stokesscher Satz.

$\vec{v} \cdot \nabla$ ist das Produkt des Geschwindigkeitsvektors mit dem Nabla-Operator und stellt alleine stehend noch keine Aussage dar. Der Differenzialoperator hat erst Bedeutung, wenn er auf einen nachstehenden Skalar oder Vektor wirkt, siehe Ergänzung 2.6, Seite 3.