1. Licht und Strahlung

Elektromagnetische Wellen    (2/4)

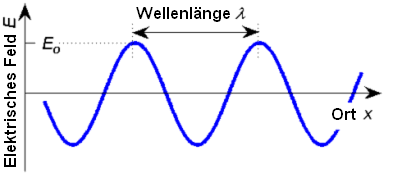
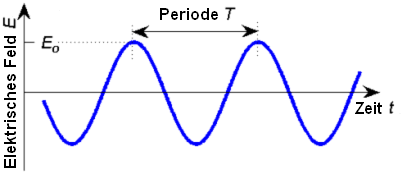
Die Eigenschaften elektromagnetischer Wellen untersuchen wir nun genauer. Wir haben auf Seite 1 dieses Kapitels gesehen, dass mono- chromatische Wellen im Raum durch die Wellenlänge λ charakterisiert werden, und in der Zeit durch die Periode T oder die Frequenz f, mit f=1/T.

Dies kann man durch eine Sinusfunktion für das elektrische Feld E darstellen, die um E=0 schwingt und deren Maximum als Amplitude Eo der Welle bezeichnet wird. Die räumliche Periodizität von E(x) über der x-Achse lässt sich daher folgendermaßen schreiben:

E(x)= E o sin2π x λ
Zoom Sign
   

                          Periodizität des elektrischen Felds E über dem Ort x.

...und die zeitliche Periodizität über der t-Achse ist:

E(t)= E o sin2π t T
Zoom Sign
   

                          Periodizität des elektrischen Felds E in der Zeit t.

Verknüpft man die räumlichen und zeitlichen Eigenschaften in einer einzigen Gleichung, so folgt schließlich für das elektrische Feld, das eine Funktion zweier Variablen x und t wird:

E(x,t)= E o sin2π( x λ − t T )
Polarisiertes Licht ↓


Der Sinus ist in Vielfachen von 2π seines Arguments periodisch. Daher nehmen die Sinusfunktionen in der linken Spalte mit

x=0, λ, 2λ, 3λ, ...  oder   x=nλ

t=0, T, 2T, 3T, ...  oder   t=nT

wobei n ganzzahlig ist, jeweils den gleichen Wert  sin2πn=0 an.

Allgemeiner gilt, dass die Auslenkung E(x,t) des elektrischen Felds immer den gleichen Wert (der nicht unbedingt gleich Null sein muss) annimmt, wenn sich die Welle längs der x-Achse um Vielfache von λ und längs der t-Achse um Vielfache von T ausgebreitet hat. Die Bedingung für einen gleichbleibenden Wert der Auslenkung ist ein konstanter Wert des Arguments (oder: der Phase) der Sinusfunktion:

x λ − t T =const.

Wir berechnen die Geschwindigkeit dieser konstanten Auslenkung durch Ableiten von x nach t:

x= λt T +λ⋅const.   ⇒    dx dt = λ T
Ableitungen ↓

Der Term dx/dt ist die sogenannte Phasengeschwindigkeit c der Welle, und es folgt:

c= λ T =fλ

Dieses Ergebnis folgt aus rein geometrischen Betrachtungen. Es gilt daher für alle Arten von Wellen, zum Beispiel Wasserwellen, Schallwellen,... Bei elektromagnetischen Wellen ist dies die Lichtgeschwindigkeit, und ihre Größe im Vakuum ist

c=2,998·108 m/s

oder circa 300 000 km/s. Die Lichtgeschwindigkeit in Luft ist geringfügig kleiner als ihr Wert in Vakuum, in Wasser ist sie etwa 225 000 km/s, und in Glas etwa 200 000 km/s. Lesen Sie mehr über die Lichtgeschwindigkeit in der Ergänzung 1.3.

Aufgabe: Laufzeit des Sonnenlichts und Mondlichts bis zur Erde ↓

Das Magnetfeld B der elektromagnetischen Welle kann durch eine zum elektrischen Feld analoge Gleichung geschrieben werden:

B(x,t)= B o sin2π( x λ − t T )

E und B schwingen senkrecht zueinander, wie in der Grafik auf der vorhergehenden Seite zu sehen ist. Darüber hinaus schwingen beide Feldgrößen senkrecht zur Ausbreitungsrichtung, hier zur x-Achse.