5. Exercises
1. Lumière et rayonnement
Ondes électromagnétiques (2/4)
Question: Temps nécéssaire à la lumière solaire et au clair de lune pour atteindre la Terre
a) La distance entre le soleil et la Terre est approximativement de 150·106 km. Combien de temps (en secondes et en minutes) faut-il à la lumière émise par le soleil pour atteindre la Terre ?
b) La distance entre la lune et la Terre est nettement plus courte: 384 000 km. Combien de temps faut-il à la lumière soleire réfléchie par la lune por atteindre la Terre ?
Réponse :
a) Le temps nécessaire à la lumière du soleil pour atteindre la terre est de
ou 8,33 minutes.
b) Pour la lumière de la lune, il est de
Question : L'année lumière et la distance à Alpha du Centaure
L'étoile la plus proche du Soleil s'appelle Alpha du Centaure. Sa distance est estimée à 4,247 années lumière. Une année lumière est la distance parcourue par la lumière en un an, une unité de longueur très souvent utilisée en astronomie. À combien de kilomètres correspond une année lumière ? À quelle distance en kilomètres se trouve Alpha du Centaure ? Vous constaterez que les années lumière sont une unité de longueur très pratique pour ne pas rendre les indications de distance des corps célestes lointains trop difficiles à gérer !
Réponse :
Une année lumière correspond au produit de la vitesse de la lumière par le temps 1 an, c'est-à-dire le temps 365 jours avec 24 heures, 60 minutes et 60 secondes chacun, soit 31,536·106 secondes.
soit 9,461·1012 km ou environ 9,5 billions de kilomètres. La distance de 4,247 années lumière d'Alpha du Centaure correspond à environ 40 000 billions de kilomètres.
Ondes électromagnétiques (4/4)
Fiche de travail: Lumière et rayonnement
Veuillez vérifier et approfondir vos connaissances sur le thème de ce chapitre à l'aide de la fiche de travail Lumière et rayonnement. Elle peut également être utilisée comme devoir de présence en classe ou comme devoir à domicile.
Photons (4/4)
Tâche : Un éclair de 1000 photons
Dans la nuit noire, nous voyons au loin le flash d'un appareil photo. Nous supposons que 1000 photons de l'éclair traversent la pupille de notre œil pour atteindre la rétine, un flash lumineux vraiment très faible. Dans la colonne de gauche ci-dessous, on peut lire qu'un œil adapté à l'obscurité peut tout juste percevoir cet éclair.
Le diamètre de la pupille est de 4 mm. La longueur d'onde de la lumière est de 500 nm (en réalité, la lumière d'un éclair est blanche). La durée de l'éclair est de 1 ms, ce qui correspond à la durée d'éclairage des flashes photo.
a) Calculez l'énergie d'un seul photon en électron-volt et celle de l'éclair composé de 1000 photons en joule.
b) Que les photons soient répartis uniformément sur la durée de l'éclair. Quelle est la puissance instantanée qui traverse la pupille ?
c) Quelle est l'irradiance en W/m2 de l'éclair à notre emplacement ?
Solutions :
a) L'énergie d'un photon est :
1 J correspond à 1,6·10-19 eV. Il devient : E = 2,48 eV. Comparez le résultat avec le graphique de la page Photons (3/4).
L'énergie totale des 1000 photons de l'éclair dans l'œil est de 0,4·10-15 J ou 0,4 fJ. (10-15 = 1 milliardième de billard = 1 femto, abréviation f)
b) L'énergie de l'éclair se produit en une milliseconde. La puissance à travers la pupille pendant la durée de l'éclair est :
ou 0,4 pW. (10-12 = 1 billionième = 1 pico, abréviation p)
Il est difficile de croire que l'œil puisse voir de tels éclairs !
c) Le rayon de la pupille est r = 2 mm. La puissance qui la traverse est de 0,4·10-12 W. L'irradiance est donc :
ou 32 nW/m2. À titre de comparaison, par ciel dégagé, l'irradiance au sol lors de la pleine lune est d'environ 3 mW/m2, le soleil au zénith rayonne à environ 1 kW/m2.
Analyse spectrale: Filtres en verre coloré (4/4)
Exercice : Réflexions
Comparez les images en noir et blanc des bandes 1 à 4 avec l'image en fausses couleurs.
- Évaluez les réflectances des surfaces terrestres végétalisées et non végétalisées et de l'eau de mer en fonction de leur luminosité.
- Consultez le tableau des bandes TM à la page précédente. Pouvez-vous confirmer les descriptions des caractéristiques?
- Étudiez vos résultats en les comparant aux informations contenues dans les pages SEOS sur
- les caractéristiques spectroscopiques de la végétation dans le tutoriel Télédétection et SIG en agriculture
- les caractéristiques spectroscopiques de l'eau de mer dans le tutoriel Ocean Colour in the Coastal Zone
- classification des images satellites dans le tutoriel Méthodes et Algorithmes de Classification
Aucune réponse n'est proposée pour cette exercise.
Supplément 1.1: Equations de Maxwell
Question 1 : Divergence et rotationnel d'un vecteur
Veuillez montrer que les équations données ci-dessus pour la divergence et le rotationnel du vecteur champ électrique sont correctes. Ces termes sont-ils des quantités scalaires ou des vecteurs ?
Réponses:
est un scalaire,
est un vecteur. , et sont les vecteurs unitaires dans la direction des coordonnées , et coordonnées.
Question 2: Gradient d'une quantité scalaire
Pour être complet, l'opérateur ∇ peut être appliqué à des quantités scalaires. Soit une fonction scalaire dans l'espace, par exemple le potentiel électrique. Le terme ∇φ désigne alors la dérivée spatiale de φ, également appelée grad φ. ∇φ est un vecteur puisque le vecteur ∇ est multiplié par le scalaire φ.
Veuillez écrire ∇φ en composantes le long des directions x, y, et z.
Réponse:
Supplément 1.2: Equations de Maxwell
Question 1 : L'opérateur de Laplace
En coordonnées cartésiennes, l'opérateur nabla
est la dérivée spatiale de premier ordre. Le produit scalaire est alors la dérivée spatiale de second ordre, l'opérateur de Laplace.
a) Veuillez montrer que l'opérateur de Laplace en coordonnées cartésiennes est :
b) Veuillez écrire l'équation d'onde du champ électrique dans ses composantes en coordonnées cartésiennes.
Réponses:
a)
b) Pour le champ électrique d'une onde dans une direction quelconque, la composante x :
et de manière correspondante pour les composantes y et z ainsi que pour les composantes du champ magnétique.
Question 2: Troisième équation de Maxwell en composantes cartésiennes
Veuillez montrer par le calcul que les vecteurs de champ
appliqués à la troisième équation de Maxwell donnent les composantes :
Réponse:
La troisième équation de Maxwell
En composants :
C'est de là que découle l'affirmation.
Supplément 1.4:
Densité d'énergie et éclairement des ondes électromagnétiques
Question 1: Champ électrique et magnétique du rayonnement solaire
Au chapitre 2 Rayonnement thermique, on montre que l'irradiance du rayonnement solaire au bord extérieur de l'atmosphère terrestre a une valeur de 1361 W/m², ce qui est appelé la constante solaire. Veuillez calculer l'intensité de champ électrique et magnétique de ce rayonnement.
Réponse :
Avec , et suit:
Le champ électrique est très fort, le champ magnétique assez faible. La cause est - comme montré dans le suppplément - la relation . Cependant, les énergies de champ du champ électrique et du champ magnétique sont égales.
On calcule ici l'amplitude d'une onde monochromatique plane, ce qui n'est pas le cas pour le rayonnement solaire avec son large spectre. Les valeurs numériques du résultat sont néanmoins valables, car les propriétés spectrales ne sont pas prises en compte dans le calcul des intensités de champ.
Supplément 1.6: La pression de radiation
Exercice 1 : La pression du rayonnement solaire
-
Au chapitre 3, section Climat et
changement climatique, nous verrons que l'irradiance du rayonnement solaire à la
périphérie de l'atmosphère terrestre a une valeur de 1361 W/m²; c'est ce
que l'on appelle la constante solaire. Quelle est la pression de radiation du rayonnement
solaire ?
Réponse :
Il s'applique :
Avec et on obtient: -
Réduit par l'absorption et la diffusion sur les molécules d'air, environ 65% du
rayonnement solaire présent à la périphérie de l'atmosphère parvient à la surface de la
terre un jour sans nuages. Comparez la pression de rayonnement présente ici avec la
pression atmosphérique au niveau de la mer, qui est en moyenne de 1013 hPa.
Réponse :
65% de la pression de radiation au bord extérieur de l'atmosphère donne à la surface de la terre. La pression atmosphérique standard de 1013 hPa est 34·109 fois plus élevée par rapport à cette pression de rayonnement. La pression de rayonnement ne joue donc aucun rôle dans les processus mécaniques à la surface de la Terre. -
Toujours au chapitre 3, section
Climat et changement climatique, le rayonnement spécifique de la photosphère du
Soleil est calculé. La photosphère est la zone de l'atmosphère solaire dans laquelle
se forme le rayonnement solaire dirigé vers l'espace. Elle s'élève à 62,9 MW/m².
Quelle est la valeur de la pression de radiation à cet endroit ?
Réponse :
Le calcul correspondant donne . La pression des gaz de la photosphère du Soleil est de 0,87 hPa dans sa partie supérieure et de 125 hPa dans sa partie inférieure. Ici aussi, la pression de radiation ne joue qu'un rôle mineur. -
Les agences spatiales étudient comment utiliser la pression de radiation pour propulser
des engins spatiaux. L'accélération obtenue avec une voile solaire réfléchissante est
certes trop faible pour des vols spatiaux habités, mais elle devrait permettre de
réaliser des missions de longue durée de petits satellites sans équipage sans
propulsion supplémentaire.
L'un des défis consiste à développer des matériaux pour des voiles à la fois légères et robustes, ainsi que les structures mécaniques nécessaires à leur déploiement dans l'espace. La dernière tentative de la NASA (dernier appel : 16.04.2025) a pour objectif de propulser une sonde d'une masse totale de 16 kg avec une voile de 80 m². L'orbite terrestre doit être héliosynchrone, de sorte que le soleil éclaire à tout moment la voile verticalement avec une constante solaire de 1361 W/m². Veuillez calculer l'accélération que l'on peut ainsi obtenir.
Réponse :
Il s'agit de
avec une surface de voile et une voile idéalement réfléchissante avec un coefficient de réflexion , et avec une masse du satellite. L'accélération est égale à,une valeur plutôt faible. La vitesse a tout de même changé de 6,27 m/s après un jour (après 86400 secondes).
Fiche de travail 1.2 : Les queues de comète
Veuillez compléter vos connaissances sur la pression de radiation avec la fiche de travail 1.2: Les queues de comète.
Tâches : Queues de comète
-
Calculez le rapport entre la gravité et la force due à la pression de radiation.
Quelle est la dépendance de ce quotient par rapport à la densité, au diamètre et
à la distance au Soleil ?
Solution :
Le rapport est proportionnel à la densité et à la taille des particules. La distance au soleil n'a pas d'importance. -
Les petits cristaux de glace dans la queue de la comète ont la densité de l'eau,
soit environ 1000 kg/m3. Pour quel diamètre de particule la force de la
pression de radiation et la force de gravité s'annulent-elles ? L'hypothèse selon
laquelle les petites particules sont repoussées par la pression de radiation et
les grandes particules sont attirées vers le Soleil est-elle correcte ?
Solution :
pourL'hypothèse est correcte. La taille critique des particules absorbantes, pour laquelle les deux forces sont égales, est d'environ 1 µm. -
Les particules des queues de comète sont manifestement plus réfléchissantes
qu'absorbantes. Comment le diamètre pour lequel les deux forces sont égales
change-t-il pour les particules idéalement réfléchissantes ?
Solution :
La force due à la pression du rayonnement sur les particules idéalement réfléchissantes double, la gravité reste la même. Par conséquent, la taille critique des particules est divisée par deux.
Supplément 1.7: Grandeurs radiatives et radiométrie
Exercice 1 : L'intensité énergétique du rayonnement solaire
Le flux énergétique du rayonnement solaire est de 387,5·1024 W. Le rayonnement est isotrope dans l'espace. La distance entre le Soleil et la Terre est de 149 589 000 km (ce qu'on appelle l'unité astronomique, UA). En raison de cette grande distance, nous pouvons considérer le soleil comme une source lumineuse ponctuelle depuis la Terre. Le rayon de la Terre est de 6371 km.
-
Quelle est la valeur de l'intensité énergétique du rayonnement solaire dans
l'espace ? Quelle est l'intensité totale du rayonnement qui atteint la Terre
ou un mètre carré de la Terre ?
Solution :
L'intensité énergétique du rayonnement à la surface du Soleil est :
Pour un émetteur isotrope, l'intensité énergétique est constante, le flux énergétique varie donc proportionnellement à l'angle solide. L'intensité énergétique qui frappe la Terre dans son ensemble et l'intensité du rayonnement pour un mètre carré de la Terre ont donc la même valeur que l'intensité énergétique du Soleil dans l'espace.
-
Calculez l'angle solide sous lequel la Terre apparaît depuis le Soleil.
Quelle est le flux énergétique du rayonnement qui atteint la Terre ?
Solution :
À partir des données relatives au rayon terrestre et à la distance entre la Terre et le Soleil, on obtient l'angle solide sous lequel apparaît la section transversale de la Terre vue depuis le Soleil :
En raison de l'isotropie du rayonnement solaire, on a :
Pour le flux énergétique qui frappe la section transversale de la Terre, on a :
-
Calculez l'angle solide sous lequel un mètre carré de la Terre apparaît depuis
le Soleil, ainsi que le flux énergétique atteignant un mètre carré de la Terre.
Comparez le résultat avec
la constante solaire
indiquée au chapitre 3, qui correspond à l'irradiance du rayonnement à
la limite extérieure de l'atmosphère terrestre.
Solution :
L'angle solide pour un mètre carré de la surface terrestre est :
Ce qui suit s'applique à nouveau :
Le flux énergétique rayonnée est :
La constante solaire est de 1361 W/m². Dans les limites de précision de cette estimation, la concordance est assez bonne.
Exercice 2 : Émetteurs isotropes
-
Augmentez l'angle solide du cône orienté vers le zénith pour former une demi-sphère
(ou un demi-espace). Quelle est alors la relation entre le flux énergétique et
l'intensité énergétique ?
Solution :
Dans le cas d'un angle solide conique orienté vers le zénith, l'angle azimutal varie de 0 à . L'angle zénithal varie de 0 à la moitié de l'angle d'ouverture :
Pour , .
-
Augmentez encore l'angle solide jusqu'à couvrir tout l'espace et calculez à nouveau la relation.
Solution :
Pour , . Ce résultat avait déjà été trouvé au début de la section consacrée à 'intensité énergétique.
Exercice 3 : Émetteurs anisotropes
L'intensité axialement symétrique d'une lampe est donnée par
-
Veuillez esquisser la répartition de l'intensité sur l'angle zénithal ϑ
de 0 à 180°.
Solution:
 Intensité de l'émetteur anisotrope en fonction de l'angle zénithal ϑ.
Intensité de l'émetteur anisotrope en fonction de l'angle zénithal ϑ. -
Calculez le flux énergétique total émise en fonction de l'intensité du rayonnement
pour ϑ = 0.
Solution:
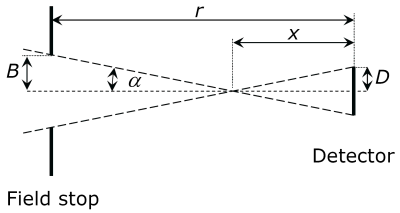
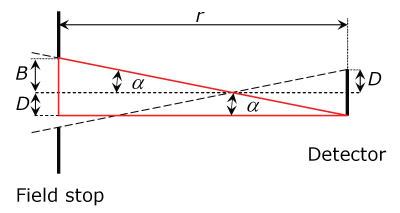
Exercice 4 : Champ visuel d'un détecteur avec diaphragme
Le détecteur et le diaphragme sont disposés à une distance r. Le rayon du détecteur est D, le rayon du diaphragme est B. est le demi-angle de champ visuel maximal possible.
Déterminez, à partir des rapports géométriques, une équation pour l'angle du champ visuel en fonction de B et D.
Remarque : trouvez un triangle rectangle qui contient l'angle ainsi que les rayons B et D.
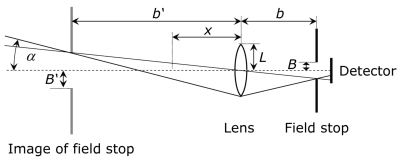
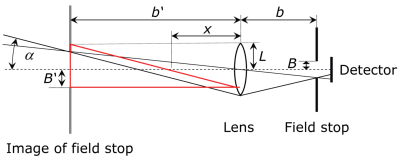
Solution:Exercice 5: Champ visuel d'un détecteur avec lentille et diaphragme
Le rendement du signal d'un détecteur avec diaphragme est très faible. On obtient un bien meilleur rendement lumineux en complétant le dispositif avec une lentille.
L'angle de réception maximal est déterminé par la lentille (de rayon L et de distance focale f) et le diaphragme à une distance b. La surface sensible du détecteur derrière le diaphragme doit être choisie de manière à ne pas limiter le trajet du faisceau. Le demi-angle de champ visuel maximal résulte de l'image du diaphragme B' à une distance b' de la lentille.
a) À partir des rapports géométriques et des équations de formation de l'image pour une lentille, déterminez une relation pour l'angle du champ visuel en fonction de L, B, b et f.
Remarque : trouvez à nouveau un triangle rectangle qui contient désormais l'angle ainsi que les grandeurs L, B' et b'. Utilisez les équations de formation de l'image par une lentille pour représenter la relation en fonction de B et b à partir de B' et b'.
b) Comment le résultat se simplifie-t-il pour b=f, c'est-à-dire lorsque l'ouverture se trouve à la distance focale de la lentille ?
Solution :a)
b)
Supplément 1.8: Émetteurs Lambert, émetteurs cosinus
Exercice 1 : Le flux énergétique des émetteurs cosinus
Les émetteurs cosinus constituent un groupe important d'émetteurs anisotropes à symétrie axiale. Leur intensité diminue avec l'augmentation de l'angle zénithal ϑ dans la plage de 0 à , conformément à cos ϑ :
Calculez le flux énergétique d'un radiateur cosinus dans un angle solide conique avec un angle zénithal
maximal ϑ' ainsi que le flux énergétique dans le demi-espace supérieur.
Solution :
Le flux énergetique dans le demi-espace supérieur :