5. Exercises
2. Rayonnement thermique
Supplément 2.1: Absorption, émission et réflexion
Tâche : Du déséquilibre à l'équilibre
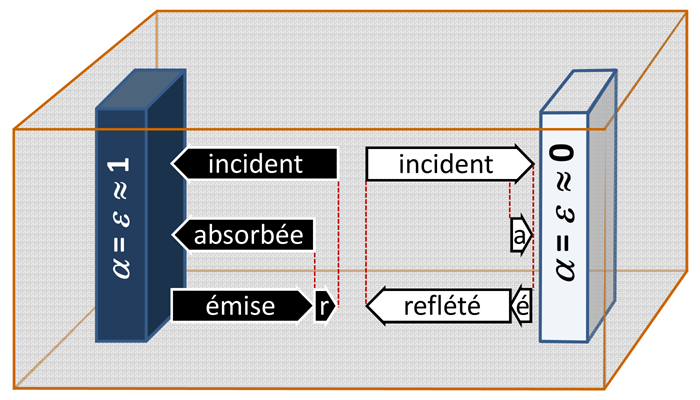
Indiquez, comme le montre le graphique, dans quelle mesure la durée des flèches changerait dans les cas suivants :
- le corps noir a une température plus élevée que le corps blanc
- le corps blanc a une température plus élevée que le corps noir.
Questions :
- Comment la longueur des flèches change-t-elle pour le rayonnement absorbé et le rayonnement émis des deux corps ?
- Quelle est la longueur des flèches pour le rayonnement entrant comme pour le rayonnement réfléchi ?
- Reconnaître comment la tendance à l'approximation des températures peut apparaître.
Réponse:
La situation est assez complexe et déroutante à première vue. Les croquis des bilans radiatifs sont très utiles pour comprendre. Quelques conseils utiles sont donnés dans ce qui suit. Ils se concentrent sur les conditions initiales de deux corps en contact, où l'un des corps a une température plus élevée et l'autre a la température de l'équilibre initial.
a) le corps noir a une température plus élevée que le corps blanc.
1 : Corps noir : l'émission et l'absorption sont plus fortes.
Corps blanc : l'émission reste la même, l'absorption est plus forte.
2 : Corps noir : l'incidence et la réflexion sont plus fortes.
Corps blanc : l'incidence et la réflexion sont plus fortes.
3 : L'émission du corps blanc reste la même, toutes les autres quantités augmentent ;
l'équilibre du corps blanc est plus fort que celui du corps noir.
b) le corps blanc a une température plus élevée que le corps noir.
1 : Corps noir : l'émission reste la même, l'absorption est plus forte.
Corps blanc : l'émission et l'absorption sont plus fortes.
2 : Corps noir : l'incidence et la réflexion sont plus fortes.
Corps blanc : l'incidence et la réflexion sont plus fortes.
3 : l'émission du corps blanc reste la même, toutes les autres quantités augmentent ;
l'équilibre du corps noir est plus fort que celui du corps blanc.
Supplément 2.6: Différentielles et dérivées
Tâche 1 : dérivées partielles et différentielles
Veuillez calculer les dérivées partielles et la différentielle totale des fonctions suivantes :
Réponses :
Les dérivées partielles :
Le différentiel :
Les dérivées partielles :
Le différentiel :
Tâche 2 : dérivées totales
Trouvez la dérivée totale de
avec et .
Réponse :
Les dérivées partielles :
Dérivés des variables :
Le différentiel total :
Tâche 3 : Dérivée partielle et différentielle totale d'un vecteur
La règle de calcul de la différentielle s'applique non seulement aux fonctions scalaires, mais aussi aux vecteurs de la même manière. Nous considérons le vecteur :
Veuillez calculer les dérivées partielles et la différentielle totale de
Réponse :
Sur la base de la définition du différentiel total :
Vous pouvez également calculer directement la différentielle totale de chaque terme de :
Tâche 4 : La température dans l'espace et le temps
La température peut être donnée par la fonction
avec :
=20°C
=0.3°C/m
=0.02°C/m³
=0.1°C/m³
=0.01°C/(m·s)
a) Quelle est la température à l'endroit = (10 m, 5 m, 2 m) à l'instant = 100 s.
b) Calculez les dérivées partielles de la température. Quelles valeurs obtenez-vous pour le lieu et à l'instant ?
c) Calculer la différence de température pour le déplacement
= (1 m, 0.5 m, 0.5 m)
au temps = 2 s plus tard.
(Nous traitons les différentielles pour l'approximation comme des quantités finies)
d) Quelles valeurs prend la température ?
Réponses :
a) = 22°C
| b) | = 0,2°C/m | ||
| = 0,4°C/m | |||
| = 3°C/m | |||
| = 0,02°C/m |
c) = 1,94°C
d) = 21,94°C
Tâche 5 : Opérateur Nabla et vecteur vitesse
L'opérateur Nabla peut être lié à un vecteur, par exemple le vecteur vitesse.
a)Représentez les termes et ` en coordonnées cartésiennes. S'agit-il de scalaires ou de vecteurs ?
b) Quelle est la signification de ces termes ? Que signifie le terme ?
Réponses :
a)
avec les vecteurs unitaires , et dans les directions des axes de coordonnées , et .
est un scalaire, est un vecteur.
b)
Le terme est également appelé divergence de la vitesse et fait référence aux sources ou aux puits de vitesse. Un bilan positif indique une source de vitesse dans la région, comme dans le cas d'un gaz en expansion par exemple. Un bilan négatif correspond à la compression d'un gaz. Mot-clé pour une lecture plus approfondie : Théorème de Gauss.
Le terme est également appelé rotation de la vitesse et désigne sa vorticité. Il est non nul en présence d'écoulements cisaillés, de tourbillons et de turbulences. Mot-clé pour une lecture plus approfondie : Théorème de Stokes.
est la multiplication du vecteur vitesse et de l'opérateur Nabla. L'opérateur différentiel doit être appliqué à une autre quantité, un scalaire ou un vecteur. Voir le supplément 2.6, page 3.
