2. Temperaturstrahlung

Die Farbe: Das Wiensche Verschiebungsgesetz

In gleicher Weise wie für die Größe der Flächen unter den Planck-Spektren schwarzer Körper interessieren wir uns nun für die Wellenlänge der größten Helligkeit. Dieses Maximum ist offenbar nur von der Temperatur abhängig, mit der Tendenz zu kleineren Wellenlängen bei wachsender Temperatur. In der Frequenzdarstellung zeigt sich eine Tendenz zu größeren Frequenzen bei wachsender Temperatur. Nach welcher funktionalen Abhängigkeit geschieht dies?

Wir gehen wie bei der Diskussion des Stefan-Boltzmann-Gesetzes von der Frequenzdarstellung der spektralen Energiedichte aus,

u f = dU df = 8πh c 3 f 3 exp{ hf / kT }−1

Die Suche nach der Frequenz fmax des Maximums der Planck-Kurve ist eine Extremalaufgabe der Analysis: Ableiten und Nullsetzen der Ableitung. Dies ist etwas schwierig, da es sich um eine transzendente Gleichung handelt: fmax findet sich gleichzeitig in erster Potenz und als Exponent der e-Funktion. Die Details der Rechnung sind in der Ergänzung 2.4 nachzulesen. Das Ergebnis ist:

f max T =5,879⋅ 10 10 1/ (s·K)

Die Frequenz des Maximums der Strahlung eines schwarzen Körpers wächst somit proportional zu seiner Temperatur.

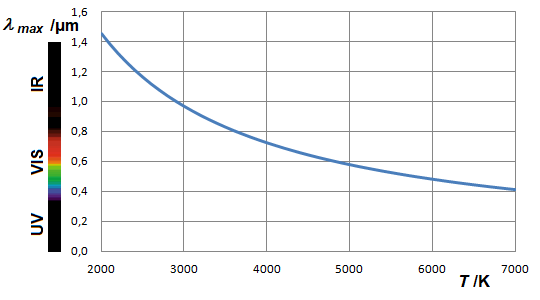
Die Lage des Maximums als Funktion der Wellenlänge ist:

λ max T=2,90⋅ 10 −3 m·K

Hier liegt eine inverse Proportionalität vor: die Maxima der Planck-Kurven als Funktion der Wellenlänge liegen auf einer Hyperbel.

Dies ist das Wiensche Verschiebungsgesetz.

Die Maxima des Planckschen Strahlungsgesetzes ändern ihre Lage im Spektrum auf besonders übersichtliche Weise: das Produkt der Wellenlänge des Maximums und der absoluten Temperatur ist konstant. Oder: der Quotient aus der Frequenz des Maximums und der absoluten Temperatur ist konstant.

 

Maximum für 2000 - 7000 K Maximum für 100 - 2000 K
Maximum für 2000 - 7000 K
Wellenlänge in µm des Strahlungsmaximums für schwarze Körper. Links: Bei Temperaturen zwischen 2000 und 7000 K. Die strahlende Sonnenoberfläche hat etwa 5800 K Temperatur. Rechts: Bei Temperaturen zwischen 100 und 2000 K. 300 K entspricht etwa Raumtemperatur.
Quelle: Rainer Reuter, Universität Oldenburg.

Kennt man ein Wertepaar, so kann die Wellenlänge oder die Frequenz des Maximums für jede andere Temperatur schon mit dem Dreisatz berechnet werden. Man muss den Zahlenwert auf der rechten Seite des Wienschen Verschiebungsgesetzes also nicht im Kopf haben. Es genügt zu wissen, dass gilt:

λ max ⋅T=const.
Aufgabe: Maxima der Planck-Kurven einiger Strahler ↓