2. Temperaturstrahlung

Die Rolle der Temperatur: Das Stefan-Boltzmann-Gesetz

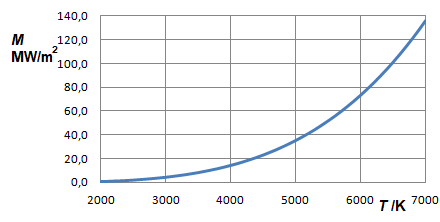
Wir interessieren uns für die Größe der Flächen unter den Planck-Spektren schwarzer Körper, die im vorherigen Abschnitt dargestellt worden sind. Offensichtlich wachsen diese Flächen mit steigender Temperatur der Strahler jäh an. In welcher Weise dies geschieht, soll durch die Ermittlung der Fläche unter den Kurven bestimmt werden.

Die Flächenberechnung ergibt sich aus dem Integral der Planck-Kurven. Geht man von der Frequenzdarstellung für die spektrale Energiedichte aus,

u f = dU df = 8πh c 3 f 3 exp{ hf / kT }−1

so erhält man durch Integration über alle möglichen Frequenzen die Energiedichte

U= ∫ f=0 ∞ u f  df= 8πh c 3 ∫ f=0 ∞ f 3 exp{ hf / kT }−1  df

Die Berechnung des Integrals ist nicht ganz einfach. Der Rechenweg wird in der Ergänzung 2.3 gezeigt. Das Ergebnis ist:

U= 8 π 5 k 4 15 c 3 h 3 T 4

Für praktische Anwendungen ist die in W/m² angegebene spezifische Ausstrahlung M eines schwarzen Körpers, beispielsweise die aus dem Öffnungsquerschnitt eines Hohlraumstrahlers austretende Leistung der Strahlung, oft aussagekräftiger als die Energiedichte in (Ws)/m³ bzw. J/m³ im Inneren des Hohlraums. Es gilt der Zusammenhang:

M= c 4 U

Dies ergibt das Stefan-Boltzmann-Gesetz:

M= 2 π 5 k 4 15 c 2 h 3 T 4 =σ T 4
Gleichungen ↓

Mit h=6,6⋅ 10 −34 Js , k=1,38⋅ 10 −23 J/K und c=3⋅ 10 10 m/s erhält man die Stefan-Boltzmann-Konstante:

σ=5,670⋅ 10 −8 W m 2 K 4
Die Strahlung wächst demnach überproportional mit der vierten Potenz der Temperatur an. Eine Verdopplung der Temperatur von zum Beispiel 300 K (Raumtemperatur) auf 600 K (327°C, die Schmelztemperatur von Blei) bedeutet eine 16fache Zunahme der Strahlung!
Gesamtstrahlung für 2000 - 7000 K Gesamtstrahlung für 0 - 2200 K
Gesamtstrahlung für 2000 - 7000 K
Gesamtstrahlung M für schwarze Körper. Links: In MW/m² bei Temperaturen zwischen 2000 und 7000 K. Die strahlende Sonnenoberfläche hat etwa 5800 K Temperatur. Rechts: In kW/m² bei Temperaturen zwischen 0 und 2200 K. 300 K entspricht etwa Raumtemperatur.
Quelle: Rainer Reuter, Universität Oldenburg.