Ergänzung 2.4: Das Wiensche Verschiebungsgesetz
Wellenlängendarstellung
Die spektrale Verteilung der Energiedichte des Strahlungsfelds eines schwarzen Körpers ist:
Die Wellenlänge des Maximums der Planckschen Strahlungskurve in Abhängigkeit von der Temperatur berechnet sich aus dem Nullsetzen der Ableitung des Strahlungsgesetzes (Extremalaufgabe). Zur besseren Übersichtlichkeit sei
Mit der neuen Variable wird das Strahlungsgesetz:
Mit der Quotientenregel wird die Ableitung:
Durch Nullsetzen und nach Kürzen findet man eine transzendente Gleichung für das Extremum :
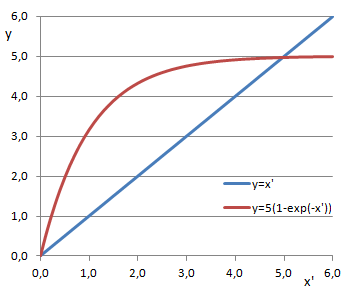
Sie kann - wie bei den meisten transzendenten Gleichungen und im Gegensatz zu algebraischen Gleichungen - nicht exakt sondern nur näherungsweise gelöst werden.
Man findet:
Mit , und folgt das Wiensche Verschiebungsgesetz:
Frequenzdarstellung
Auch hier kann man von dem in der linken Spalte berechneten Maximum der Wellenlängendarstellung nicht unmittelbar mit der Beziehung auf das Maximum schließen. Die Grafiken der Planck-Kurven in der Wellenlängen- und der Frequenzdarstellung zeigen auch, dass ihre Maxima mit nicht zusammen gehören.
Die Rechnung muss daher auch in diesem Fall vom Planckschen Strahlungsgesetz in der Frequenzdarstellung ausgehen. Der Rechenweg ist ganz vergleichbar dem in der linken Spalte. Der Vollständigkeit halber sind die entsprechenden Gleichungen unten angegeben.
Die spektrale Energiedichte des schwarzen Körpers als Funktion der Frequenz ist:
Das Strahlungsgesetz mit der neuen Variablen :
Ableitung nach der Frequenz:
Die transzendente Gleichung für die Berechnung des Extremums
mit der Lösung .
Das Wiensche Verschiebungsgesetz wird so: