2. Introduction aux méthodes mathématiques
Probabilités (1/2)
La probabilité Pr{} nous donne un mécanisme qui nous permet de travailler avec les incertitudes. C'est important car cela apporte un moyen d'analyser l'incertitude associée à un évènement ou une séquence d'évènements.
Les probabilités ont toujours une valeur comprise entre 0 et 1.
| Pr{} = 0: | Il n'y a aucune chance que l'évènement arrive |
| Pr{} = 1: | L'évènement va certainement arriver |
| Pr{} = 0,5: | Il y a autant de chance que l'évènement arrive que de chances qu'il n'arrive pas |

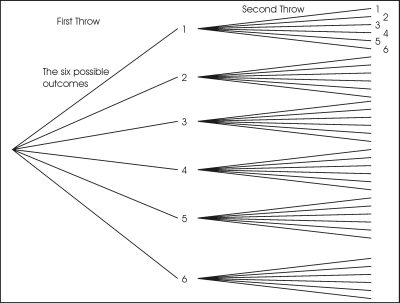
Prenons l'exemple du lancer de dés. Si l'évènement consiste en deux lancers de dés, il y a six résultats possibles pour le premier lancer (la première partie de l'évènement), et pour chacun de ces résultats, il y a six résultats possibles pour le deuxième lancer. Il y a donc 36 résultats possibles au total. On a la même probabilité d'arriver à chacun de ces résultats si les dés ne sont pas truqués, donc chaque combinaison à une probabilité de 1/36 :
Avec des dés, on a la même probabilité d'obtenir chaque nombre. Ce n'est pas toujours le cas dans la vie. Considérons une course de chevaux, pour laquelle la probabilité de chacun des six chevaux de gagner la course est donnée dans la table ci-dessous.
| Cheval | Probabilité course 1 |
Probabilité course 2 |
|---|---|---|
| Raddish | 0,05 | 0,1 |
| Mums the word | 0,25 | 0,22 |
| Pie in the sky | 0,30 | 0,04 |
| Doughboy | 0,06 | 0,35 |
| Atlantis Star | 0,28 | 0,18 |
| Felty | 0,06 | 0,11 |
| Total | 1,00 | 1,00 |
Dans cette table, on suppose les deux courses indépendantes, et les différences de probabilités sont probablement dues à des conditions de course différentes, comme par exemple des distances parcourues différentes ou des conditions du sol inégales. De cette table, on peut voir que la probabilité pour Doughboy de gagner les deux courses est de 0,06 · 0,35 = 0,021.
Questions
- Quelle est la probabilité d'obtenir un six en jetant un dé ?
- Quelle est la probabilité d'obtenir une somme égale à six en jetant deux dés ?