2. Introduction aux méthodes mathématiques
Covariance et corrélation (2/2)
Dans cette matrice de corrélation, les éléments de la diagonale depuis le haut à gauche jusqu'en bas à droite valent tous 1. Ils ont cette valeur car ils contiennent la variance pour une variable dans la matrice de covariance, qui est divisée par l'écart-type de la colonne et de la ligne, c'est-à-dire qu'ils sont divisés deux fois par l'écart-type.
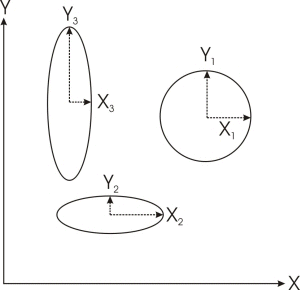
Quand deux variables sont non-corrélées, les éléments en dehors de la diagonale valent zéro dans les matrices de covariance et de corrélation. Nous pouvons représenter la matrice de covariance en deux dimensions, formant des cercles ou des ellipses. Pour ce faire, nous pointons les valeurs moyennes pour une classe dans l'espace à deux dimensions, puis nous pointons l'écart-type de chaque coté de cette valeur moyenne, dans la direction de l'axe approprié. Si les données ne sont pas corrélées, alors les ellipses ou les cercles ressembleront à ceux montrés à gauche sur cette page. Si les écarts-types sont les mêmes dans les deux dimensions représentées, nous obtiendrons un cercle. Sinon, nous obtiendrons une ellipse, dont le demi grand axe sera parallèle à l'axe comportant les plus grandes valeurs d'écart-type.
S'il y a covariance ou corrélation, nous obtiendrons des ellipses, orientées selon un certain angle par rapport aux deux axes, angle dépendant de la covariance entre les deux variables. La figure de la page précédente montre la covariance pour deux échantillons différents ayant des données corrélées. L'échantillon 1 (X1,Y1) a des données positivement corrélées, donc une augmentation de x entraine normalement une augmentation de y. L'échantillon 3 (X3,Y3) a des données corrélées négativement, donc une augmentation de x entraine une diminution de y. l'orientation des axes des ellipses indique si la corrélation est positive ou négative. La corrélation vaut zéro quand le demi grand axe de l'ellipse coïncide soit avec l'axe des x, soit avec l'axe des y. La corrélation atteint son maximum de 1 quand le demi grand axe est à 45° par rapport aux deux axes.
Il y a un concept mathématique de corrélation et de covariance, qui peut être calculé grâce à des calculs matriciels.
Si les diagrammes de dispersions de fréquences montrent des structures diagonales par rapport aux axes x et y, les deux variables (ou les canaux dans le cas d'une image satellite) dépendent l'une de l'autre, elles sont corrélées.