2. Introduction aux méthodes mathématiques

Covariance et corrélation (1/2)

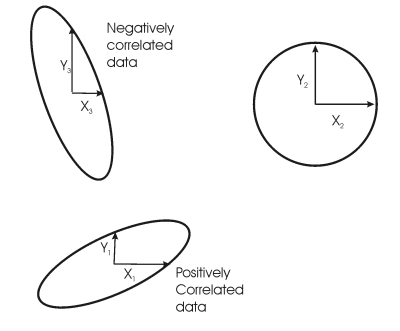
Nous avons vu que des données peuvent être corrélées, de façon à ce que l'augmentation d'un paramètre correspondent normalement à l'augmentation du second paramètre. Dans ce cas, la distribution de fréquences montre une structure linéaire allant en diagonale depuis le bas à gauche vers le haut à droite. Comment mesurer cette corrélation, et comment la représenter ?

Pour ce faire, nous allons adapter l'équation de la variance que vous avez vue dans le chapitre sur les mesures d'étendue, et nous appellerons cette adaptation la covariance. Nous obtiendrons la corrélation à partir de la covariance.

Rappelez-vous l'équation de la variance :

De façon similaire, la covariance entre les variables x et y est donnée par :

Maintenant, nous pouvons construire ces variances et covariances comme une matrice :

Dans cette matrice, il n'y a que deux variables (x et y), c'est donc une matrice (2,2). Vous pouvez faire cela pour n'importe quel nombre de variables, donc pour n variables, vous obtiendriez une matrice de covariance (nn,n). Dans une matrice de covariance, comme vous pouvez le voir, les éléments de la diagonale (depuis le haut à gauche jusqu'au bas à droite) sont la variance, et les valeurs en dehors de la diagonale sont les valeurs de la covariance.

La corrélation entre x et y est donnée par

Nous pouvons construire la matrice de corrélation en divisant les valeurs de chaque rangée par l'écart-type dans cette rangée et en divisant ensuite les valeurs dans chaque colonne par l'écart-type dans cette colonne. Pour deux variables, on obtient