Ergänzung 7.3: Raman-Streuung (4/6)

Quantentheorie

Makroskopische Massen, die mit Federn verbunden sind, können - in Grenzen - mit beliebigen (kontinuierlich verteilten) Amplituden und entsprechenden Energien schwingen. Bei atomaren Massen ist dies anders: die Schwingungsenergien sind diskret (quantisiert). Dass dies bei Molekülen so ist und die erlaubten Schwingungszustände konstante Energieabstände besitzen, haben wir bereits auf Seite 2 der Ergänzung über Fluoreszenz gesehen.

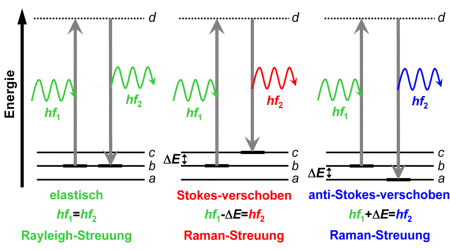
In der rechts gezeigten Abbildung sind drei Schwingungszustände (a, b, c) eingetragen. Sie unterscheiden sich in ihrer Energie um den Wert ΔE. Es wird angenommen, dass sich das Molekül im mittleren Energiezustand b befindet.

Die Quantentheorie stellt Licht als Teilchen - Photonen - dar. Die Modelle des Lichts als elektromagnetische Welle und Teilchen sind in der SEOS-Lerneinheit Spektren der Erde ausführlich vorgestellt. Trifft ein Photon auf das Molekül, so kann es absorbiert werden, wenn die Photonenenergie geeignet ist, das Molekül in einen höheren elektronischen Zustand zu führen; dies ist ebenfalls in der Ergänzung über Fluoreszenz beschrieben.

Ist die Photonenenergie jedoch zu gering, um einen höheren Energiezustand zu erreichen, dann nimmt das Molekül einen sehr kurzlebigen Zustand (d) ein, von dem aus es sehr schnell - typisch nach Femtosekunden (1 fs=10^-15 s) - wieder in einen tieferliegenden Zustand übergeht. Der Zustand (d) ist nicht stationär und wird daher als virtuelles Niveau bezeichnet, in der Grafik ist er als gestrichelte Linie dargestellt.

Entscheidend ist nun, auf welchen tieferliegenden Zustand das Elektron zurückfällt.

• Ist es der Zustand, von dem aus die Anregung erfolgte (in der Grafik: Zustand b), wird ein Photon gleicher Energie emittiert. Seine Richtung stimmt nicht mit der Richtung des kurzzeitig absorbierten Photons überein. Da die Richtung des Photons sich ändert, bezeichnet man den Vorgang als Lichtstreuung, als Rayleigh-Streuung. Da die Photonenenergie erhalten bleibt, handelt es sich um eine elastische Streuung.
• Ist es ein Zustand höherer Schwingungsenergie (in der Grafik: Zustand c), wird ein Photon mit einer um ΔE geringeren Energie emittiert. ΔE verbleibt als Schwingungsenergie im Molekül. Die Streuung ist inelastisch und entspricht der Stokes-verschobenen Raman-Streuung.
• Ist es ein Zustand niedererer Schwingungsenergie (in der Grafik: Zustand a), wird ein Photon mit einer um ΔE größeren Energie emittiert. Die Schwingungsenergie des Moleküls nimmt um ΔE ab. Die Streuung ist ebenfalls inelastisch und entspricht der anti-Stokes-verschobenen Raman-Streuung.

Wechselwirkung eines Photons mit einem Molekül: aus dem durch das kurzzeitig absorbierte Photon erreichten virtuellen Energieniveau (gestrichelte Linie) geht das Molekül in den Ausgangszustand oder in einen Schwingungszustand größerer oder kleinerer Energie zurück. Entsprechend ist die Energie des emittierten Photons gleich (elastische Rayleigh-Streuung), kleiner oder größer (Raman-Streuung) als die Energie des kurzzeitig absorbierten Photons.

Nach dem Modell der elektromagnetischen Wellen sollte die Stokes- und anti-Stokes-verschobene Raman-Streuung die gleiche Intensität aufweisen. Im Photonenmodell wird verständlich, weshalb dies nicht der Fall ist. Die Besetzungszahlen der Schwingungszustände (a), (b) und (c) ergeben sich aus der in Kapitel 2 dargestellten Boltzmann-Verteilung, wonach tieferliegende Energiezustände mit höherer Wahrscheinlichkeit besetzt sind als höherliegende Zustände. Da sich demnach die meisten Moleküle im Zustand (a) befinden, können sie nach der Photonenabsorption einen tieferliegenden Zustand gar nicht erreichen; dies ist nur Molekülen möglich, die sich in den Zuständen (b) oder (c) befinden.

Ausgehend von der Energie E=hf der Photonen (mit dem Planckschen Wirkungsquantum h und der Frequenz f der entsprechenden elektromagnetischen Welle) und dem energetischen Abstand ΔE der molekularen Schwingungszustände ergeben sich die in der Grafik oben angegebenen Gleichungen zur Energiebilanz dieser Streuvorgänge in sehr übersichtlicher Weise.

Zahlenwerte der Energie könnten in Joule (J), Wattsekunden (Ws) oder in Elektronenvolt (eV) (das in der SEOS-Lerneinheit Spektren der Erde erklärt wird) angegeben werden. In der Spektroskopie werden bevorzugt Wellenzahlen $\tilde{\nu }$ genutzt, die in der Einheit cm^-1 angegeben werden. Sie entsprechen bis auf Naturkonstanten der Energie:

Der Zahlenwert einer Wellenzahl $\tilde{\nu }$ berechnet sich demnach aus dem Kehrwert der in Zentimetern angegebenen Wellenlänge λ.