Ergänzung 7.3: Raman-Streuung (5/6)
Die Raman-Streuung des Wassers
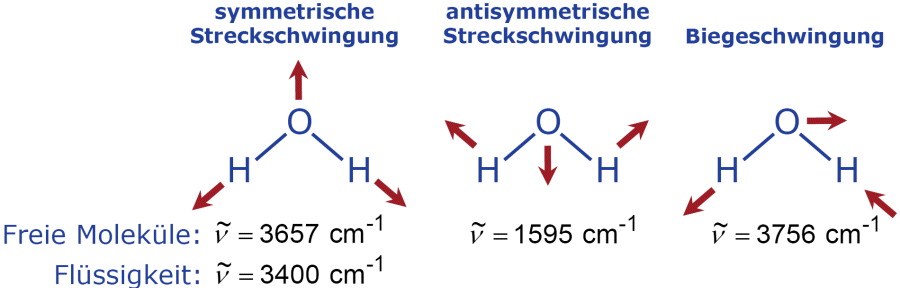
Die auf Seite 3 dieser Ergänzung gezeigten Schwingungsformen des Wassermoleküls können wir nun statt mit Schwingungsfrequenzen f auch in Wellenzahlen angeben.
Die Raman-Linien der Wassermoleküle in flüssigem Wasser sind - verglichen mit den Raman-Linien des Wasserdampfs - spektral breit. Dies wird durch Stöße der Moleküle mit ihren Nachbarn in der Füssigkeit und die damit einhergehenden Störungen der Energiezustände verursacht. Man bezeichnet sie als Raman-Banden. Aus der Energiebilanz der Stokes-verschobenen Raman-Bande (siehe Grafik in der rechten Spalte auf der vorherigen Seite)
folgt mit und die Beziehung
in der die Wellenlänge des absorbierten Lichts und die Wellenlänge der Stokes-verschobenen Raman-Bande ist. wird als Anregungswellenlänge und als Raman-Wellenlänge bezeichnet.
Die folgende Grafik zeigt die Lage der Raman-Wellenlängen des flüssigen Wassers bei drei unterschiedlichen Anregungswellenlängen.
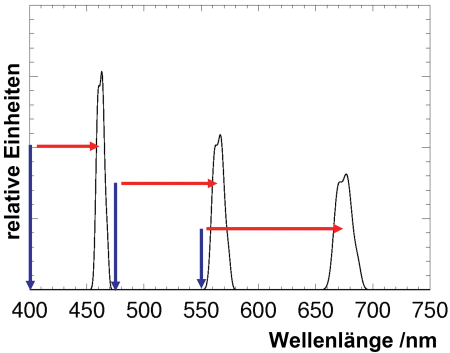
Aus der Grafik wird deutlich, dass der Abstand der Raman-Wellenlänge zur Anregungswellenlänge nicht konstant bleibt, sondern mit wachsender Anregungswellenlänge steigt. Nach der Energiebilanzgleichung ist nicht die Differenz dieser Wellenlängen, sondern die Energiedifferenz beziehungsweise die Wellenzahl konstant.