Ergänzung 3.1: Polarisation elektromagnetischer Wellen, eine Einführung
Ein erster Ansatz
Auf Seite 2 des Abschnitts über elektromagnetische Wellen haben wir Gleichungen für das elektrische und das magnetische Feld einer ebenen monochromatischen Welle entwickelt:
Da die Sinusfunktion in periodisch ist, zeigen die Gleichungen anschaulich die Periodizität mit der Wellenlänge λ und der Periodendauer T. Statt dieser Größen werden oft andere Parameter genutzt, mit denen sich die Gleichungen etwas kürzer schreiben lassen, da sie den Faktor enthalten. Dies sind:
- die Wellenzahl
- die Kreisfrequenz
Damit wird:
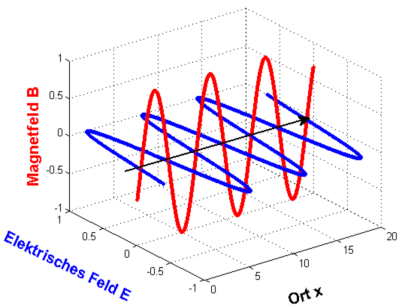
In einer Grafik sieht die Welle so aus:
Nur Transversalwellen - zum Beispiel die elektromagnetischen - können polarisiert sein. Bei Longitudinalwellen - zum Beispiel Schallwellen - gibt es keine Polarisation.
In der oben gezeigten Grafik ist nichts über die Richtungen des elektrischen und des magnetischen Felds ausgesagt (abgesehen davon, dass sie senkrecht aufeinander und senkrecht zur Ausbreitungsrichtung stehen): es fehlen die y- und z-Koordinaten, um die Richtungen der Feldstärkevektoren darzustellen.
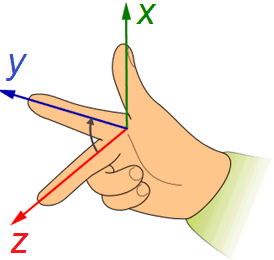
Wir untersuchen nun eine Welle, die sich in einem dreidimensionalen rechtshändigen -Koordinatensystem in Richtung x ausbreitet. Es wird nur das elektrische Feld betrachtet; die Ergebnisse gelten entsprechend auch für das senkrecht zum elektrischen Feld schwingende Magnetfeld.
Der Feldvektor steht senkrecht auf der Ausbreitungsrichtung x. Er wird in Komponenten in den Richtungen y und z zerlegt:
und sind die Amplituden. Die Größe kennzeichnet eine Phasenverschiebung zwischen den beiden Komponenten. Für eine monochromatische Welle ist konstant, die beiden Teilwellen sind daher zueinander kohärent.
Die wichtigsten Polarisationsarten mit ihren Schwingungsformen, ist eine ganze Zahl:
| Bedingung | Polarisationsart |
|---|---|
| linear längs der y-Achse | |
| linear längs der z-Achse | |
| linear diagonal im ersten und dritten Quadranten der y,z-Ebene | |
| linear diagonal im zweiten und vierten Quadranten der y,z-Ebene | |
| rechts zirkular: die Feldvektoren drehen rechts, wenn man der Welle entgegen sieht. Animation der drehenden Vektorspitzen, das E-Feld ist blau, das B-Feld ist rot wiedergegeben |
|
| links zirkular: die Feldvektoren drehen links, wenn man der Welle entgegen sieht | |
| rechts elliptisch: die Feldvektoren drehen rechts, wenn man der Welle entgegen sieht. Animation der drehenden Vektorspitzen, das E-Feld ist blau, das B-Feld ist rot wiedergegeben |
|
| unpolarisiert, natürliches Licht |
Natürliches Licht ist nicht monochromatisch sondern spektral breit verteilt, und ändert sich permanent statistisch. Die y- und z-Komponenten sind daher nicht zueinander kohärent.
Teilpolarisiertes Licht setzt sich aus einem Anteil polarisierten und einem Anteil unpolarisierten Lichts zusammen. Dies charakterisiert man durch den Polarisationsgrad: