2. Introduction aux méthodes mathématiques

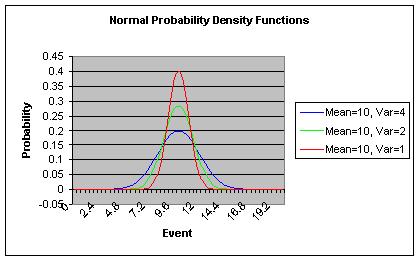
La distribution normale

Nombre de types de données on des valeurs pouvant varier dans une plage continue de valeurs. Ce type de données est appelé données continues. La distribution binomiale ne peut être utilisée pour les données continues.

La distribution normale peut être utilisée pour de nombreuses applications impliquant des données continues. La distribution normale a pour avantage que sa forme ne dépend que de la moyenne et de la variance.

Il y a un certain nombre de choses importantes à savoir à propos de la Fonction de Densité de Probabilité Normale :

  1. La FDP normale est une fonction des valeurs de moyenne et de variance.
  2. La PDF normale a un seul maximum, et ses valeurs sont symétriques autour de ce maximum.
  3. Le maximum de la PDF normale est sa valeur moyenne, mode et médiane.
  4. La valeur moyenne peut prendre n'importe quelle valeur numérique ; négative, zéro ou positive.
  5. La fonction s'étend à l'infini dans les deux directions depuis la moyenne, mais atteint évidemment des valeurs extrêmement faibles.
  6. L'écart-type détermine la largeur et la hauteur de la courbe. Des valeurs plus grandes donnent une courbe plus large et plus plate.
  7. Le point d'inflexion de chaque côté de la courbe se trouve à un écart-type de la moyenne.
  8. L'aire totale sous la courbe vaut 1,0, comme pour toutes les FDP continues.
  9. Les probabilités sont données par les aires sous la courbe, pour un point de départ et d'arrivée donné. Certaines probabilités utiles sont reprises ci-dessous :
    • 68,26% du temps, une variable normale aléatoire (x) aura une valeur de maximum un écart-type à la moyenne.
    • 95,44% du temps, une variable normale aléatoire aura une valeur de maximum deux écarts-types à la moyenne.
    • 99,72% du temps, une variable normale aléatoire aura une valeur de maximum trois écarts-types à la moyenne.
Zoom Sign
Normal Probability Distribution Function
Fonctions de Distribution Normale de Probabilités

L'équation d'une FDP normale est

F(x)=N(μ, σ 2 )= e {− ( x−μ ) 2 2 σ 2 } σ 2π

Dans cette équation, on peut voir que les paramètres sont la moyenne (μ) et la variance (σ2), pour une variable x. La FDP Normale Standard a une moyenne de 0 et une variance unitaire :

f( z ) = N( 0,1 )=  e − z 2 /2 2π

Où z =  ( x−μ ) /σ afin qu'une Table de Probabilités pour une FDP normale standard puisse être utilisée pour n'importe quelle FDP normale en transformant les valeurs de x de la FDP normale en valeurs de z de la FDP normale standard.

Questions:

  1. Quelle est la probabilité d'obtenir une valeur à moins d'un écart-type de la moyenne de Pr{ ( −1≤z≤1 )| N( 0,1 ) } ? Regardez dans la table de la FDP normale standard à 1,00 et vous obtenez 0,3413. Cette valeur va du centre vers un des côtés de la distribution, donc il faut la doubler pour obtenir l'étendue de 0,6826.

  2. Quelle est la probabilité d'obtenir une valeur dans une plage de 8 à 12 dans la FDP normale, N(10, 4) ? Convertissez d'abord x = 8 et 12 en valeurs de z.

  3. Quelle est la valeur de la probabilité, Pr{ ( 10≤x≤14 )| N( 10,4 ) } ?

  4. Quelle est la valeur de la probabilité, Pr{ ( 9≤x≤14 )| N( 10,4 ) } ?

  5. Quelle est la valeur de la probabilité, Pr{ ( 11≤x≤15 )| N( 10,4 ) } ?

  6. Quelle est la valeur de la probabilité, Pr{ ( x>12 )| N( 10,4 ) } ?
Exercices, tutoriaux et réponses