2. Introduction aux méthodes mathématiques
Fonctions de densité de probabilité
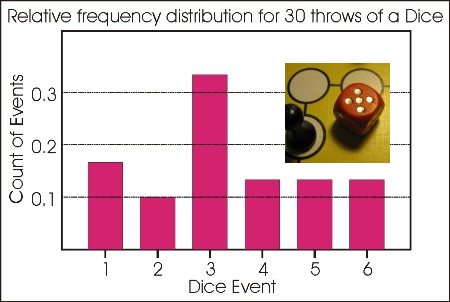
Nous avons vu les distributions de fréquences d'un échantillon, desquelles on peut obtenir les, histogrammes qui expriment la proportion de lancers qui ont donné chaque valeur du dé. Une distribution de fréquences relatives est aussi une fonction de densité de probabilité (FDP) de l'échantillon, car les valeurs sont aussi les probabilités que chaque évènement arrive, en fonction de l'échantillon de données.
Quoi qu'il en soit, nous savons que la probabilité d'obtenir n'importe quel chiffre avec un dé est égale à 1/6 à chaque lancer. Quand la probabilité de chaque évènement est égale, les données ont une fonction de densité de probabilité uniforme et donc la distribution théorique pour un lancer de dé est une distribution uniforme d'une valeur de 1/6. Si l'on prenait un échantillon assez grand, les probabilités obtenues à partir de cet échantillon seraient proche de la probabilité théorique.
La Fonction de Densité de Probabilité pour un échantillon de données est unique à ce jeu de données. Ce que l'on veut généralement, c'est une FDP qui peut s'appliquer à plusieurs échantillons. Dans ce cas, une FDP obtenue à partir d'un échantillon et utilisée pour en analyser d'autres peut amener des erreurs significatives, et sera donc difficile à utiliser. On peut souvent trouver une FPD, comme une distribution théorique, pour un jeu de données, ou comme approximation d'un jeu de données.
Reprenons notre dé. Théoriquement, chaque chiffre a une probabilité égale de sortir. La fonction de densité de probabilité théorique pour un lancer de dé est donc une distribution uniforme de valeur 1/6, et donc 30 lancers devraient donner 5 fois chaque chiffre. Cela n'est pas arrivé dans notre échantillon du Premier Chapitre, puisque ce n'était qu'un échantillon de données. En pratique, plus l'échantillon est grand, plus il sera proche de la distribution uniforme.
| Valeur | Nombre d'apparitions dans l'échantillon | Probabilité d'apparition dans l'échantillon | Probabilité théorique |
|---|---|---|---|
| 2 | 0 | 0,000 | 0,028 |
| 3 | 1 | 0,033 | 0,056 |
| 4 | 3 | 0,100 | 0,083 |
| 5 | 2 | 0,067 | 0,111 |
| 6 | 6 | 0,200 | 0,139 |
| 7 | 5 | 0,167 | 0,167 |
| 8 | 2 | 0,067 | 0,139 |
| 9 | 6 | 0,200 | 0,111 |
| 10 | 2 | 0,067 | 0,083 |
| 11 | 3 | 0,100 | 0,056 |
| 12 | 0 | 0,000 | 0,028 |
| Total | 30 | 1,000 | 1,000 |
La Fonction de Densité de probabilité pour le lancer de deux dés n'est pas une distribution uniforme, donc comment pouvons-nous la calculer ?
La probabilité d'obtenir un deux n'est possible que si un 1 est obtenu sur chaque dé. Nous savons que la probabilité d'obtenir un 1 avec un dé est de 1/6, donc la probabilité d'obtenir deux fois 1 est de (1/6)·(1/6) = (1/36). On peut obtenir un trois avec un 2 et un 1 ou avec un 1 et un 2... Les deux cas ont une probabilité de 1/36, donc les deux ensemble nous donnent une probabilité de 2/36. Vous pouvez maintenant vérifier les valeurs données dans la table pour chaque nombre.
Les Fonctions de Densité de Probabilité ont une valeur limitée dans les analyse, car on ne peut les décrire précisément en n'utilisant que quelques paramètres, et parce qu'elles changeront chaque fois qu'un nouvel échantillon est pris. Pour des évènements discrets, on peut souvent dériver une FDP théorique applicable aux données, comme nous l'avons fait pour le lancer d'un ou deux dés. Cela n'est pas toujours possible avec des données continues. Quoi qu'il en soit, il existe quelques FDP standard, qui sont utiles si certaines conditions sont remplies. Nous allons voir deux Fonctions de Densité de Probabilité parmi les plus largement utilisées dans la leçon suivante.