Supplement 4.8: An Experiment on the Light Scattering of Water

Light scattering by water, an example of Rayleigh scattering

The absorption coefficient of liquid water is less than 1/m for all visible wavelengths. In the blue range, water is particularly transparent, there the absorption coefficient is about 0.02/m.

The scattering coefficient of water is about a factor of 10 smaller in the blue area. This is due to the small size of the molecule compared to the wavelength of light: its diameter is about 2 Å or 2·10^-10 m (the Ångström, with the unit sign Å, is a common unit of length in atomic physics). Water molecules are therefore an example of particles that are characterised by Rayleigh scattering.

Here we are investigating how a water sample scatters the light from a laser.

The experimental set-up

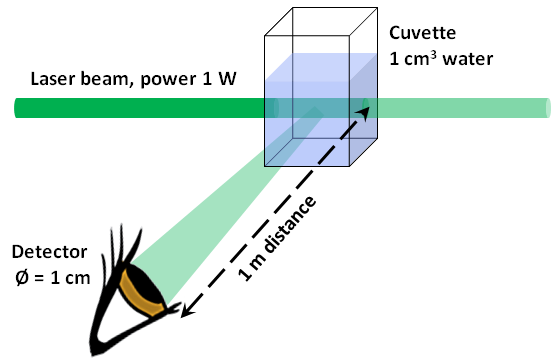
A water-filled cuvette is illuminated with a blue-green laser beam. The wavelength is 500 nm, the radiation power is 1 W (if you would like to reproduce the experiment experimentally: this laser would by no means be eye-safe, please exercise extreme caution).

At 90° against the direction of the laser beam, we first observe with the eye the scattered light produced on the water. Let the illuminated and visible water volume be V = 1 cm³.

Experimental set-up for the measurement of light scattering from a water sample.
Source: Rainer Reuter, University of Oldenburg, Germany.

Then we attach a photodiode for a quantitative measurement at a distance of r = 1 m from the cuvette and also at 90°. Let the diameter of the photosensitive area be d = 1 cm. At 500 nm, let the sensitivity of the photodiode, i.e. the photocurrent (in amperes) of the diode generated by an optical power (in watts), be assumed to be S = 0.5 A/W.

Scattering properties of water

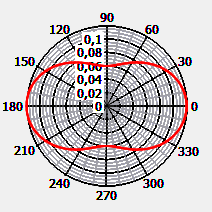
Very small particles scatter the light symmetrically in the front and back half-space. This is characteristic for Rayleigh scattering of small particles. If the scattering angle measured relative to the direction of the laser beam is denoted by θ, the scattering function for unpolarised light is given by the equation

β (θ) = β (90 °) (1 + {cos}^{2} θ)

Polar diagram of the phase function versus angle θ for particles with the diameter 2 Å, with the refractive index n = 1.33 and for light of wavelength 500 nm. The phase function is equal to the scattering function β divided by the scattering coefficient b. We will calculate the value of b in the right-hand column.
Created with MieSimulatorGUI, Version 1.3, last access: 30 March 2023.

The literature value of the scattering function for the scattering angle 90° at the wavelength 500 nm is (Zhang & Hu, 2021):

β (90 °) = 1.38 \cdot 10^{- 4} \frac{1}{m sr}

Equations ↓

The molar mass of water is about 18 g, correspondingly the molar volume is about 18 cm³. The number of particles in the mole is given by the Avogadro constant 6·10²³. The number of water molecules in 1 m³ is then:

N = \frac{6 \cdot 10^{23}}{18 \cdot 10^{- 6} m^{3}} = 3.3 \cdot 10^{28} \frac{1}{m^{3}}

The differential cross-section of the scattering at 90° results in:

σ (90 °) = \frac{β (90 °)}{N} = 4.14 \cdot 10^{- 33} \frac{m^{2}}{sr}

The brightness at the eye

The intensity of the scattered light follows from the values of the scattering function β of the water and the irradiance E of the laser on the illuminated water volume V according to

I = β E V

where E = 1 W/cm² and V = 1 cm³. The optical power at the eye or detector results from this intensity multiplied by the solid angle Ω at which the eye or detector appears as seen from the scattering water:

P = I (90 °) Ω = β (90 °) E V \frac{π d^{2} / 4}{r^{2}}

Substituting all values gives the optical power P ≈ 10^-10 W or 0,1 nanowatt. Can the eye still see this?

In order to assess this, it is useful to go over to the photon image of light. A dark-adapted eye can perceive about every 50th photon striking the retina as a faint flash of light. For monochromatic light, the relationship between optical power and the corresponding photon number is as follows:

P = N_{P h o t o n} E_{P h o t o n}

where N_Photon is the number of photons per second, and the photon energy E_Photon = hc/λ. h is the Planck constant and c is the light velocity. It follows N_Photon ≈ 250· 10⁶ or 250 million photons per second.

The signal of the detector

The photocurrent of the photodiode results from the incident optical power and from its sensitivity, which has been assumed to be S = 0.5 A/W above. It becomes:

I_{p h o t o} = S P = 0.5 \cdot 10^{- 10} A

or 50 picoampere. Electrical multimeters only reach into the microampere range at best, so you need a much more sensitive ammeter. Such devices are called picoammeters.

The scattering coefficient

If the scattering function is integrated over the entire space, the scattering coefficient results:

\begin{array}{l} b = \int_{Ω = 4 π} β d Ω = 2 π \int_{θ = 0}^{π} β (θ) sin θ d θ \\ = 2 π β (90 °) \int_{θ = 0}^{π} (1 + {cos}^{2} θ) sin θ d θ = 16 \frac{π}{3} β (90 °) \end{array}

Inserting gives: $b = 2.3 \cdot 10^{- 3} /m$

Over a distance of 1 m, the laser beam loses 2.3 per mille of its brightness due to scattering. The decrease in brightness in the cuvette of our experiment, which is only one centimetre long, is practically negligible.

The total scattering cross-section (integrated over the entire space) becomes:

σ = \frac{b}{N} = 7 \cdot 10^{- 32} m^{2}

Compared to their geometric cross-sectional area, the molecules thus only shadow a very small part of the brightness of the laser beam.

In fact, there are some additional influencing variables in the light scattering of water. Temperature, pressure and - in the case of seawater - salinity play a role. And density fluctuations occur in the liquid, which also contribute to the scattering. The publication of Zhang & Hu, 2021 provides detailed information on this.