4. Absorption and scattering

Some mathematics

We are starting with a focus on the smallest – infinitesimal – scale within an absorbing substance that is illuminated from the left hand side. The light has an intensity of $I$ at the point $x$. Only an infinitesimal step $\text{d}x$ further, at the point $x+\text{d}x$, the intensity has decreased by an infinitesimal amount $\text{d}I$, so it can be described as $I-\text{d}I$.

Light propagates from the left to the right hand side in an absorbing medium. At the point x the intensity equals I, whereas it decreased to I-dI at the point x+dx.

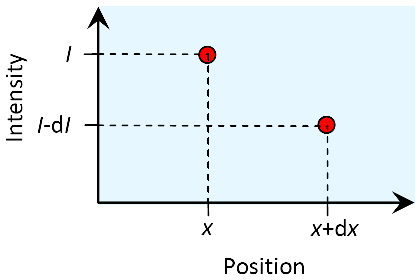
The decline $-\text{d}I$ is assumed to be proportional to $I$ and $\text{d}x$:

On top of that, the decline will be dependant on the absorption features of the substance. These special properties will be characterised by the absorption coefficient a, what makes proportionality become an equation:

Through transformation, the following differential equation is obtained:

which now has to be solved (or: integrated). When said in words, the solution is easy to find:

  "Questioned is the intensity $I$, ..."
  on the left: "...of which the differentiation with respect to $x$..."
  on the right: "... results in $I$ with the additional factor $-a$ ."

The function that is able to do that is the exponential function: It persists when being derivated or integrated. A possible approach for solving the problem is thus:

what leads to the initial differential equation when being differentiated with respect to $x$:

Therefore the exponential equation is the way to the solution.

At the point $x=0$ the intensity shall equal $I_o$ (Let this be the intensity at the beginning, the previous approach yields $x=0$ for the value of 1), and has to be completed on the right hand side of the equation. This leads to the final solution:

Lambert's law: The intensity of light decreases exponentially in function of the distance x. That is shown in the following pictures through the example of the absorption of laser light by green pigments in plants.

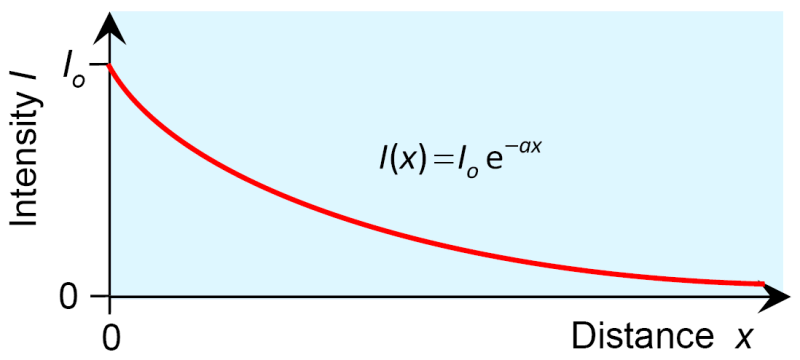
This is Lambert's law: The intensity of light decreases exponentially on its way through an absorbing medium, while the decline depends on the medium's absorption coefficient $a$.

405 nm 532 nm 650 nm Chlorophyll absorption

Chlorophyll a was extracted from plant's leaves using alcohol. The greenish solution (in a glass cuvette) is lighted by laser beams from the left. Chlorophyll absorbs blue light. In consequence, the brightness of the blue beam (wavelength of 405 nm) decreases from left to right. The red glow is created by the red fluorescence chlorophyll emits when absorbing blue light. The green laser beam (532 nm) shows no perceptable decline of brightness, the red laser beam (650 nm) only a small one. As it is influenced by the absorption of chlorophyll at different wavelengths, the laser beams decline differently at different points of the cuvette.
Source of the Chlorophyll a absorption spectrum: PhotochemCAD. The spectrum shows the molar decadic absorption coefficient, which will be explained in Supplement 4.1.

The dimension of the absorption coefficient is an inverse length. Depending on its value, it may be given in different units:

• for the cloud-free atmosphere mostly in 1/km,
• for waters in 1/m,
• for highly absorbing materials (e.g. spots of environmental pollution through crude oil) in 1/μm.