1. Light and Radiation
Photons (4/4)
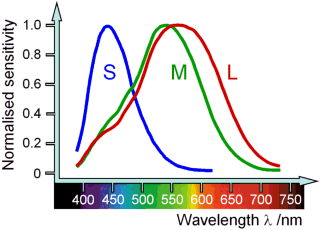
How are we able to see colour? There are three types of light receptors called cones found on the retina of the human eye which enable us to see colour during daylight.
The S-cones (S for short) perceive blue light with a highest sensitivity at 420 nm. The M-cones (M for medium) perceive green light, their sensitivity is highest at 535 nm. The L-cones (L for long) are responsible for seeing red although their maximum sensitivity lies somewhere in the yellow region at about 560 nm.
In the photon model, light is distributed among the different cones depending on the energy of the photons. Through a chemical reaction, the photons absorbed by the cones produce electric signals which are sent through the optic nerve to the brain. The brain receives the signals and interprets them according to cone type, thus producing the colour impressions we perceive.
This makes the physiological colours perceived by the eye different from the physical colour spectrum also shown in the above diagram. For example, the human eye can not directly perceive the physical colour ‘yellow’ which has a monochromatic wavelength of 560 nm, but must produce it by combining the signals sent by the M and L-cones.
Now, how do we define energy and intensity? In the photon model, the photon energy is:
with the Planck constant h and the frequency of light f. We have seen that the photon energy is essential for chemical reactions as they occur, e.g., in the cones of the eye when perceiving colours, and also for the release electrons from metal surfaces, which we denoted as as the photoelectric effect. The wavelength of light is not relevant, it is not included in the equation for the photon energy.
What happens when light is transmitted through air into another transparent material such as glass or water? The light is refracted and partially reflected. Its colour, however, remains unchanged in the other material. The energy of the photons remains unchanged, too. Hence, the colour of light is connected to the energy of its photons!
As a result obtained in the section on electromagnetic waves, we obtained a relationship between the speed of light, the frequency and wavelength as
In the wave model, the photon energy - as shown in the equation given above - is connected to the frequency f of light. The energy of photons remains invariant in different transparent materials, and therefore this holds also with the frequency. Since the speed of light c in transparent materials is smaller than the speed of light in vacuum co, it follows:
where λ is the wavelength in the transparent material and λo is the wavelength in vacuum. The wavelength of light does not remain constant when light is transmitted into a transparent medium but rather decreases in the same degree as the speed of light.
Hence, it is rather inaccurate to define colours by using the wavelength of light! Instead, it would be correct to use photon energies or frequencies! However, in everyday language we are always using the wavelength.
Within the wave model we obtained the same result in supplement 4 following a much more complicated calculus.