Ergänzung 2.6: Differenziale und Ableitungen (4/4)

Die Geschwindigkeit einer Strömung als Beispiel eines Vektors

Die bisher entwickelte Systematik gilt nicht nur für skalare Größen wie etwa die Temperatur, sondern auch für Vektoren, zum Beispiel für den Geschwindigkeitsvektor. Ersetzen wir in der Gleichung

\frac{d T}{d t} = \frac{\partial T}{\partial t} + \vec{v} \cdot \nabla T

$T$ durch $\vec{v}$ , so wird:

\frac{d \vec{v}}{d t} = \frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v}

Die Begriffe 'Lagrange- und Euler-Darstellung' sowie 'konvektiver Term' werden hier in gleicher Weise genutzt. Auffällig ist allerdings die Klammersetzung. Was bedeutet sie?

Der Term $\vec{v} \cdot \nabla T$ im Beispiel zur Temperatur ist das Skalarprodukt der beiden Vektoren $\vec{v}$ und $\nabla T$ . Auf die Reihenfolge der Produktbildung kommt es hier allerdings nicht an: man kann auch zunächst $\vec{v} \cdot \nabla$ berechnen und das skalare Ergebnis auf $T$ anwenden.

Der Ausdruck $\nabla \vec{v}$ wäre jedoch nicht definiert, weshalb es hier auf die Reihenfolge der Produktbildung ankommt. Dies verdeutlicht die Klammer im Term $(\vec{v} \cdot \nabla) \vec{v}$ . Zunächst wird das Produkt

\vec{v} \cdot \nabla = u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z}

gebildet und das Ergebnis - ein Skalar - mit $\vec{v}$ multipliziert,

(\vec{v} \cdot \nabla) \vec{v} = u \frac{\partial \vec{v}}{\partial x} + v \frac{\partial \vec{v}}{\partial y} + w \frac{\partial \vec{v}}{\partial z}

in Komponenten:

\begin{array}{l} (\vec{v} \cdot \nabla) u = u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \\ (\vec{v} \cdot \nabla) v = u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \\ (\vec{v} \cdot \nabla) w = u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \end{array}

Aufgabe 5: Nabla-Operator und Geschwindigkeitsvektor ↓

Der Nabla-Operator lässt sich mit einem Vektor, zum Beispiel mit der Geschwindigkeit, verknüpfen.

a) Stellen Sie die Ausdrücke $\nabla \cdot \vec{v}$ und $\nabla \times \vec{v}$ ` in kartesischen Koordinaten dar. Sind sie Skalare oder Vektoren?

b) Welche Bedeutung haben diese Ausdrücke? Was bedeutet der Ausdruck $\vec{v} \cdot \nabla$ ?

Die Lösung finden Sie auf dieser Seite.

Die totale Ableitung der Geschwindigkeit wird somit in Komponenten:

\frac{d u}{d t} = \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z}

\frac{dv}{d t} = \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z}

\frac{dw}{d t} = \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z}

Dies sind die kinematischen Grundgleichungen der physikalischen Beschreibung von Strömungen: sie präzisieren den Begriff der Beschleunigung deformierbarer Medien wie etwa Luft und Wasser.

Werden Kräfte als Ursachen von Beschleunigungen in den Gleichungen ergänzt, erhält man die hydrodynamische Bewegungsgleichung. Gehört zu den Kräften auch die Reibung, so ist das Ergebnis die Navier-Stokes-Gleichung der Hydrodynamik.

Mechanik der Massenpunkte und der deformierbaren Medien ↓

Wird das "Wie" des Ablaufs der Bewegung eines Körpers dargestellt, so bezeichnet man dies als Kinematik der Bewegung. Zur Darstellung der Bewegung des Schwerpunks eines Körpers nutzt man seine Lage $\vec{r} (t)$ im Raum, seine Geschwindigkeit $\vec{v} (t) = \frac{d \vec{r} (t)}{d t}$ und seine Beschleunigung $\vec{a} (t) = \frac{d \vec{v} (t)}{d t} = \frac{d^{2} \vec{r} (t)}{d t^{2}}$ .

Berücksichtigt man auch das "Warum" einer Bewegung, so kommen die Kräfte zum Tragen, welche die Bewegung beeinflussen; dies stellt dann die Dynamik der Bewegung dar. Die Newtonsche Bewegungsgleichung

\vec{F} = m \frac{d \vec{v}}{d t} = m \vec{a}

ist ein Beispiel, in dem ein Körper mit der Masse $m$ durch eine äußere Kraft $\vec{F}$ die Beschleunigung $\vec{a}$ erfährt.

Bei deformierbaren Körpern, d.h. Gasen und Flüssigkeiten, führt die Bewegung des Schwerpunktes selten zu einem gewünschten Ergebnis. Vielmehr sind die Details der Bewegung des ausgedehnten und meist komplex geformten Mediums einschließlich der Vorgänge im Inneren von Interesse. Die Bewegungsgleichung wird ganz vergleichbar formuliert, allerdings nicht mit der Masse, sondern mit der Massendichte $ρ = \frac{d m}{d V}$ , also der Masse pro Volumen, die räumlich und zeitlich variieren kann. Entsprechend betrachtet man nicht die äußeren Kräfte selbst, sondern ihre Kraftdichte:

\frac{d \vec{F}}{d V} = ρ \frac{d \vec{v}}{d t} = ρ \vec{a}

Ein infinimesimales Massenelement erfährt wie der Schwerpunkt eines festen Körpers die Beschleunigung $\frac{d \vec{v}}{d t}$ . Hier setzt sie sich jedoch additiv aus einer lokalen Beschleunigung $\frac{\partial \vec{v}}{\partial t}$ und dem Einfluss $(\vec{v} \cdot \nabla) \vec{v}$ der umgebenden Massenelemente, also dem konvektiven Term, zusammen.

Die folgende Abbildung zeigt die Trajektorien von Oberflächendriftern, in diesem Beispiel mit einem Farbkeil, der die Driftgeschwindigkeit in m/s angibt. Zu erkennen ist, dass die Driftgeschwindigkeiten sehr variabel sind und auch auf der offenen See hohe Werte annehmen. Dies ist ein Beispiel der Lagrange-Darstellung von Driftgeschwindigkeiten.

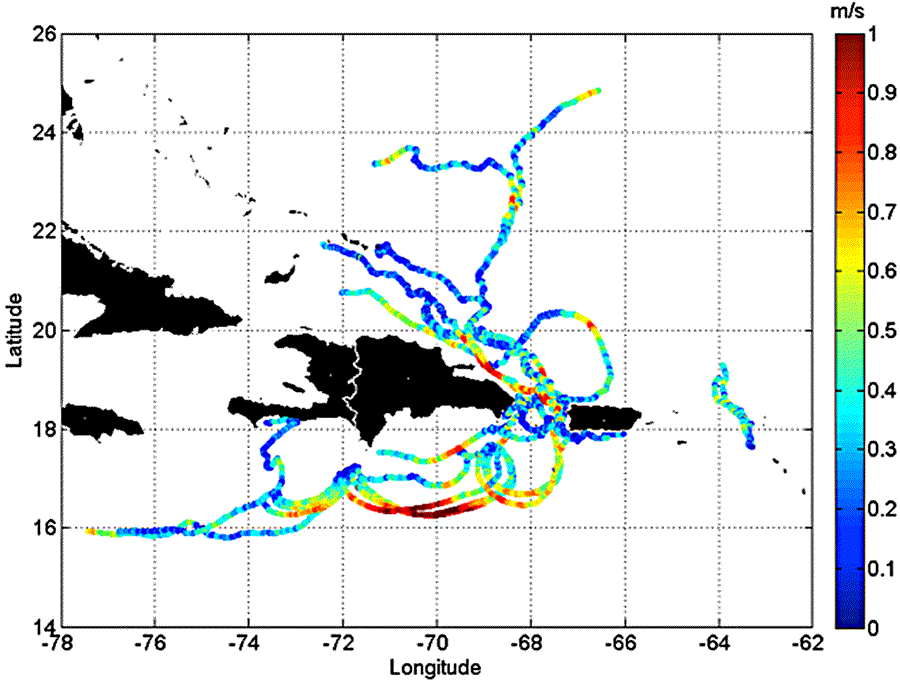
Driftwege bei der Dominikanischen Republik und Puerto Rico

Trajektorien von 18 Oberflächendriftern im Bereich der Dominikanischen Republik und Puerto Rico. Der Farbkeil zeigt die Driftgeschwindigkeit in m/s.
Quelle: Caribbean Coastal Ocean Observation System (Caribbean IOOS).

Die nächste Abbildung zeigt eine Zeitreihe der Meeresströmung über zwei Tage im niedersächsischen Wattenmeer bei Spiekeroog. Aufgetragen ist der Betrag der Strömungsgeschwindigkeit, die durch die halbtägige Gezeit geprägt wird, und die durch das Spiekerooger Seegatt vorgegebene Nord-Süd-Richtung der Strömung. Dies ist ein Beispiel für die Euler-Darstellung einer Strömungsgeschwindigkeit.

Strömungsdaten bei einer Messstation im Seegatt von Spiekeroog. Mitte und unten: Betrag und Richtung der Strömung. Oben rechts: Vektoren der Strömungsgeschwindigkeit aufgetragen in einem Polarkoordinatendiagramm.

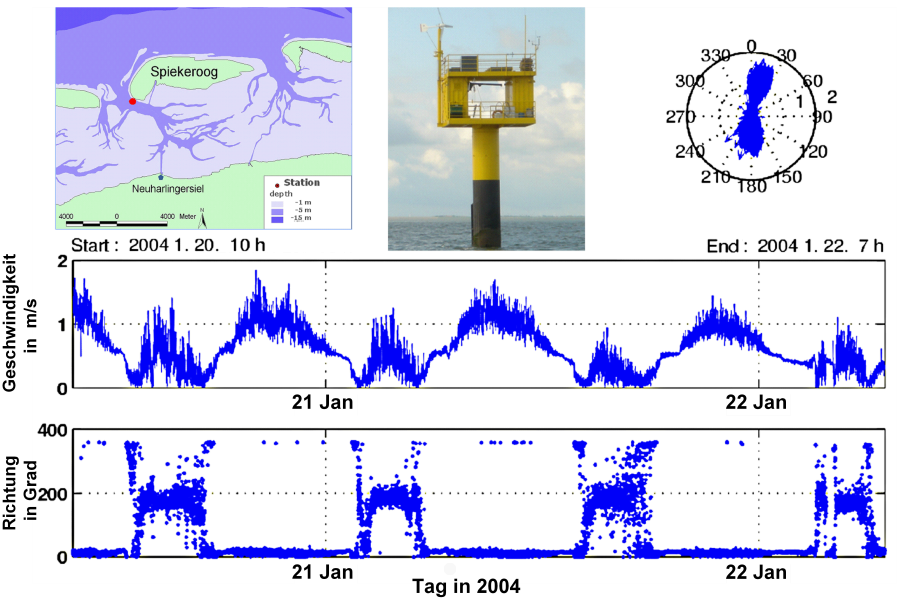
Mit der von Satelliten aus genutzten Radar-Altimetrie können aus der gemessenen Topografie der Ozeanoberfläche die globalen Meeresströmungen bestimmt werden. Auch hierzu findet sich auf der Seite externer Links ein Verweis zu einem mehrjährigen Video des NASA Scientific Visualization Studio als Beispiel einer Lagrange-Darstellung der Meeresströmungen.

Spektren der Erde

Ergänzung 2.6: Differenziale und Ableitungen (4/4)

Die Geschwindigkeit einer Strömung als Beispiel eines Vektors