Ergänzung 2.6: Differenziale und Ableitungen (3/4)
Die Temperatur als Beispiel ... (Fortsetzung)
Die totale Ableitung der Temperatur lässt sich angeben, wenn die Ortsvariablen bzw. der Ortsvektor eine Funktion der Zeit sind:
Für die Temperatur in bewegter Luft oder in strömendem Wasser ist dies offensichtlich der Fall, wenn der Ortsvektor die zeitlich veränderliche Lage eines definierten Luft- oder Wasserelements kennzeichnet. Damit folgt:
Hierbei wird ausgenutzt, dass
die Geschwindigkeitskomponenten der Strömung in Richtung , und sind.
In Vektorschreibweise gilt:
oder, mit dem Geschwindigkeitsvektor :
In der Hydro- und Aerodynamik sowie in der Meteorologie und Ozeanographie haben sich für die Terme dieser Gleichung besondere Begriffe herausgebildet:
-
ist die Lagrange-Darstellung: die Ortskoordinaten und die Zeit sind Variable, d.h. ein Luft- oder
Wasserelement wird auf dem Weg durch den Raum zeitlich verfolgt und die Änderung seiner Temperatur beschrieben.
Experimentell kann dies beispielsweise mit einem Thermometer in einem auftriebsneutralen Ballon realisiert werden, welcher dem Wind folgt wie ein Luftelement; in einem Gewässer oder im Meer ist es ein auftriebsneutraler Drifter, der der Strömung des Wassers folgt. -
ist die Euler-Darstellung: Variable ist die Zeit, der Ort wird festgehalten. Hier wird die Temperatur
der vorbeiströmenden Luft oder des Wassers gemessen, weshalb sie auch lokale Ableitung genannt wird.
Experimentell wird dies mit ortsfest betriebenen Sensoren, zum Beispiel mit einer fest montierten Wetterstation oder einer in einem Gewässer verankerten Messboje erreicht. Beispiele von Temperaturdaten im Meer, die an einer festen Messstation im niedersächsischen Wattenmeer bei Spiekeroog gewonnen wurden, werden in der Lerneinheit zur Zeitreihenanalyse ausführlich diskutiert. - wird als konvektiver Term bezeichnet: er enthält den Temperaturgradienten, d.h. die räumliche Veränderlichkeit der Temperatur, der mit der Strömungsgeschwindigkeit als Faktor gewichtet wird. Addiert mit der Euler-Darstellung ergibt der konvektive Term die Lagrange-Darstellung des Temperaturfelds.
Die für die Wettervorhersage wichtigen Wetterballone verhalten sich nicht nach der Lagrange-Darstellung: sie schweben nicht, sondern steigen mit kräftigem Auftrieb bis etwa 30 km Höhe auf, um Höhenprofile der Lufttemperatur und anderer Messgräßen zu registrieren.
Drifter im Ozean erfüllen sehr viel besser die Anforderungen an die Lagrange-Darstellung: sie treiben wie im Global Drifter Program mit der Strömung an der Wasseroberfläche, oder sie schweben in 1000 bis 2000 m Tiefe wie etwa die Argo Floats. Diese so genannten Lagrange-Drifter können über ein bis zwei Jahre autonom eingesetzt werden, bis sie gewartet werden müssen.
Das Bild unten zeigt Driftwege (auch als Trajektorien bezeichnet), die südlich von Puerto Rico mit Driftern aufgenommen wurden. Die Messungen dienten der Untersuchung der Meeresströmung, Temperaturdaten wurden nicht registriert. Sie zeigen, wie veränderlich sich Strömungen auch in einem kleinen Küstengebiet verhalten können.
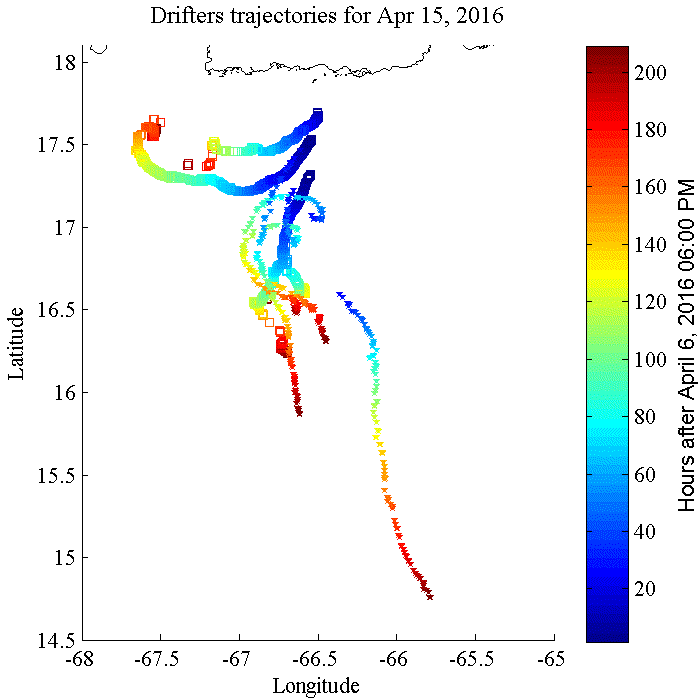
Quelle: Caribbean Coastal Ocean Observation System (Caribbean IOOS).
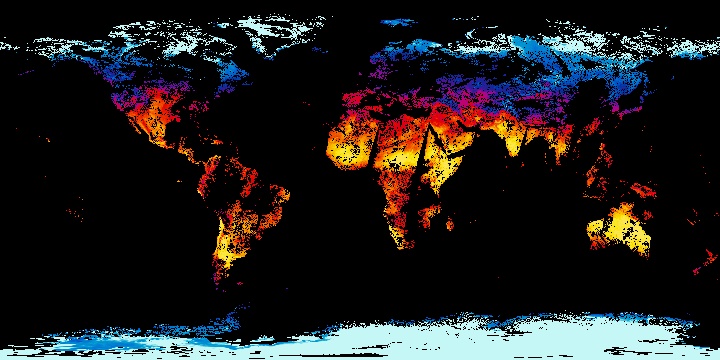
Die folgenden globalen Karten der Oberflächentemperatur des Festlands sind Schnappschüsse, wie in der Infobox 'Weniger Variable' am Ende der vorherigen Webseite erläutert. Die Zeit kommt als veränderliche Variable nicht vor, vielmehr werden die während eines oder mehrerer Tage gemessenen Temperaturen in einer Karte gemeinsam wiedergegeben. Solche Momentaufnahmen werden als synoptische Darstellung, d.h. als Gesamtdarstellung gleichzeitig gemessener Daten bezeichnet; eine Gleichzeitigkeit ist im Fall globaler Datensätze allerdings nur näherungsweise zu erreichen.

Quelle: NEO - NASA Earth Observations.
Erzeugt man aus zeitlich aufeinander folgenden Momentaufnahmen ein Video, so entspricht das Ergebnis der Lagrange-Darstellung, da sowohl die räumlichen Koordinaten (hier: in zwei Dimensionen) wie auch die Zeit berücksichtigt werden. Auf der Seite der externen Links findet sich ein Verweis zu einem mehrjährigen Video der Landoberflächentemperatur des NASA Earth Observatory als Beispiel einer Lagrange-Darstellung globaler Temperaturen.