Supplement 2.6: Differentialen en afgeleiden   (3/4)

De temperatuur als voorbeeld ... (cont.)

De totale afgeleide van de temperatuur kan worden gegeven als de ruimtelijke variabelen resp. de positievector functies van de tijd zijn:

Dit is duidelijk het geval voor bewegende lucht of stromend water als de positievector de in de tijd veranderende positie van een gedefinieerd lucht- of waterelement aangeeft. Hieruit volgt:

Hierbij zijn

de snelheidscomponenten van de stroming in de richtingen $x$, $y$ en $z$.

In vectornotatie:

of met de snelheidsvector $\overrightarrow{v}=(u,v,w)$:

In de hydro- en aerodynamica, zoals in de meteorologie en oceanografie, zijn specifieke woorden gevormd voor deze termen:

• $\frac{\text{d}T}{\text{d}t}$ is de Lagrangiaanse vorm: de ruimtelijke coördinaten en de tijd zijn variabel, d.w.z. een lucht- of waterelement wordt tijdsgewijs geobserveerd terwijl het door de ruimte beweegt en zijn temperatuurverandering wordt beschreven.
  In experimenten kan dit bijvoorbeeld worden uitgevoerd door middel van een thermometer in een drijfvermogenneutrale ballon die als een luchtelement de wind volgt; in wateren of de zee is het een drijfvermogenneutrale drifter die de waterstroom volgt.
• $\frac{\partial T}{\partial t}$ is de Euleriaanse vorm: de tijd is variabel terwijl de positie vast is. De temperatuur van de passerende lucht- of waterstroom wordt in deze tijd gemeten. Daarom wordt het ook wel de lokale afgeleide genoemd.
  n experimenten kan dit in de praktijk worden gebracht met behulp van sensoren die op een vaste plek zijn gemonteerd, bijvoorbeeld met een geïnstalleerd weerstation of een gegevensboei die op de grond is bevestigd. Voorbeelden van temperatuurgegevens van de zee die zijn verzameld op een geïnstalleerd meetstation in de Waddenzee in Nedersaksen, vlakbij het eiland Spiekeroog, worden uitgebreid besproken in de SEOS Tutorial over tijdreeksanalyse.
• $\overrightarrow{v}\cdot \nabla T$ wordt de convectieve term: genoemd: deze omvat de temperatuurgradiënt, d.w.z. de ruimtelijke verandering van temperatuur die wordt vermenigvuldigd met de snelheidsvector. Toegevoegd aan de Euleriaanse vorm levert de convectieve term de Lagrangiaanse vorm van het temperatuurveld op.

Weerballonnen, die belangrijk zijn voor de weersvoorspelling, gedragen zich niet volgens de Lagrangiaanse benadering omdat ze niet in de lucht zweven maar tot ongeveer 30 km de lucht in gaan om verticale profielen van de luchttemperatuur en andere parameters op te nemen.

Drifters in de oceaan voldoen veel beter aan de eisen: ze drijven zoals in het Global Drifter Program met de stroming mee op het wateroppervlak of ze drijven op 1000 tot 2000 m diepte zoals de Argo Floats doen. Deze zogenaamde Lagrangiaanse drifters kunnen een tot twee jaar autonoom werken voordat ze onderhoud nodig hebben.

De afbeelding hieronder toont drijfpaden (ook wel trajectoriën genoemd) die in het zuiden van Puerto Rico met drifters werden geregistreerd. De metingen dienen om de oceaanstroming te onderzoeken, temperatuurgegevens werden niet verzameld. Ze laten zien hoe variabel de stroming kan zijn, zelfs in een klein kustgebied.

Trajecten van drifters die op hetzelfde tijdstip zijn gestart vanaf verschillende locaties in het zuiden van Puerto Rico aan de oppervlakte (rechthoeken) en op 18 m diepte (sterren). De gekleurde schaal toont de tijd in uren na het loslaten van de drifters.
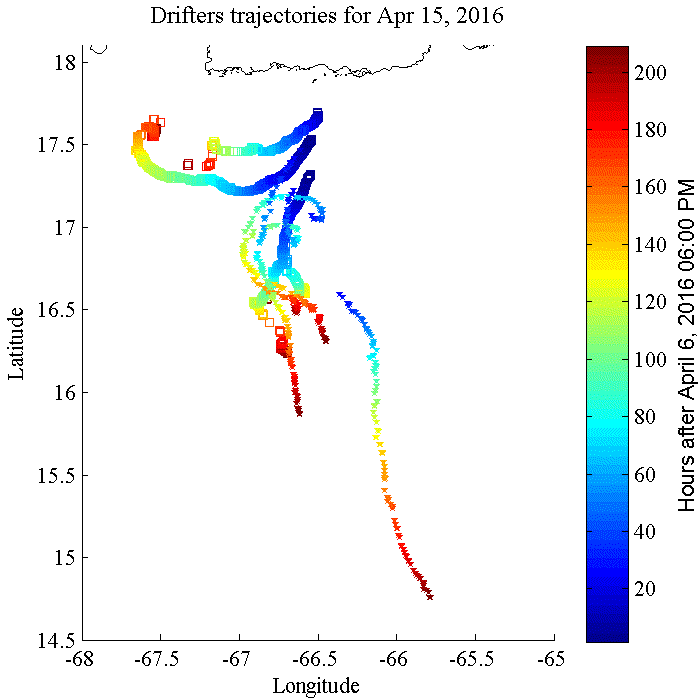
Bron: Caribbean Coastal Ocean Observation System (Caribbean IOOS).

De volgende mondiale kaarten van de landoppervlaktetemperatuur zijn momentopnamen zoals uitgelegd in de infobox 'Minder variabelen' aan het einde van de vorige pagina. De tijd verschijnt niet als variabele. In plaats daarvan worden de temperaturen die gedurende één dag of meerdere dagen zijn gemeten, samengevoegd in één kaart. Dergelijke momentopnamen worden synoptische weergave genoemd, d.w.z. als een algemene weergave van verschillende gegevens die op hetzelfde moment zijn gemeten; in het geval van wereldwijde gegevensverzamelingen kan dit doel niet volledig worden bereikt.

22 feb 2017 18-26 feb 2017 feb 2017

Temperaturen op het aardoppervlak. Links: 22 februari 2017. Midden: weekgemiddelde van 18 tot 26 februari 2017. Rechts: maandgemiddelde van februari 2017. Mozaïekweergave van gegevens van de MODIS-spectrometer op NASA's Terra-satelliet bij daglicht. Het wordt duidelijk dat gegevens van één enkele dag niet genoeg zijn om het hele aardoppervlak af te beelden; de onvolledige dekking van de satelliet en bewolking dwarsbomen de temperatuurmeting aan het oppervlak.
Bron: NEO - NASA Earth Observations.

Als je een video maakt van chronologische momentopnames, krijg je een Lagrangiaanse presentatie omdat zowel de ruimtelijke coördinaten (hier: in twee dimensies) als de tijd in beschouwing worden genomen. Op de pagina Links vind je een verwijzing naar een video over landoppervlaktetemperaturen over meerdere jaren gepubliceerd in NASA's Earth Observatory als voorbeeld van een Lagrangiaanse presentatie van wereldwijde temperaturen.