2. Rayonnement thermique
La couleur : la loi de déplacement de Wien
La zone située sous les spectres des corps noirs nous intéresse au même titre que les longueurs d'onde pour lesquelles les spectres de Planck atteignent leur valeur maximale. Ce maximum semble dépendre uniquement de la température, avec une tendance à des longueurs d'onde plus petites lorsque la température augmente. Si l'on considère les spectres de Planck comme une représentation de la fréquence, on constate une tendance à l'augmentation de la fréquence des maxima lorsque la température augmente. Sur quelle dépendance fonctionnelle cela repose-t-il ?
Nous partons de la représentation en fréquence de la densité spectrale d'énergie, comme nous l'avons fait pour la loi de Stefan-Boltzmann.
La recherche du maximum de la loi de radiation est un problème d'extremum de l'analyse mathématique : dériver et mettre à zéro la dérivée. Ceci est quelque peu difficile car il s'agit d'une équation transcendante : est trouvé en première puissance et simultanément comme l'exposant de la fonction e. Le calcul détaillé se trouve dans le supplément 2.4.
Le résultat est le suivant :
La fréquence du maximum de rayonnement d'un corps noir augmente proportionnellement à sa température.
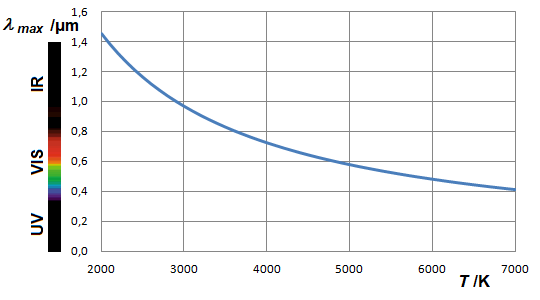
La position du maximum en fonction de la longueur d'onde résulte d'un calcul analogue, voir supplément 2.4. Le résultat est le suivant :
Dans ce cas, on trouve une proportionnalité inverse : les maxima du graphique de Planck en fonction de la longueur d'onde suivent une hyperbole.
C'est ce qu'on appelle la loi de déplacement de Wien..
Source: Rainer Reuter, Université d'Oldenburg, Allemagne.
Connaissant une paire de valeurs, la longueur d'onde de la fréquence du maximum peut être calculée pour toutes les autres températures par la règle de trois. Il n'est donc pas nécessaire de mémoriser la valeur à droite de la loi de déplacement de Wien. Il suffit de savoir que :