2. Rayonnement thermique

Le rôle de la température : la loi de Stefan-Boltzmann

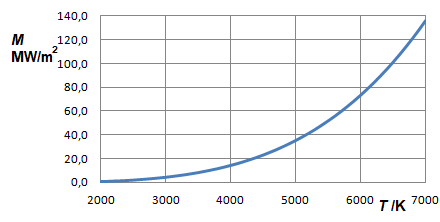
Nous nous intéressons à la zone située sous les spectres de Planck des corps noirs, dont il a été question dans la section précédente. Ces zones augmentent évidemment avec l'augmentation de la température de l'émetteur. La façon dont cela se produit sera trouvée par la détermination de l'aire sous les graphiques.

Le calcul de la surface résulte de l'intégration des graphiques de Planck. En supposant que la représentation de la fréquence de la densité spectrale d'énergie

u_{f} = \frac{d U}{d f} = \frac{8 π h}{c^{3}} \frac{f^{3}}{exp {h f / k T} - 1}

Par intégration, on obtient la densité d'énergie de toutes les fréquences possibles

U = \int_{f = 0}^{\infty} u_{f} d f = \frac{8 π h}{c^{3}} \int_{f = 0}^{\infty} \frac{f^{3}}{exp {h f / k T} - 1} d f

Le calcul de l'intégrale peut être légèrement difficile. La procédure est présentée dans le supplement 2.3. Le résultat est le suivant :

U = \frac{8 π^{5} k^{4}}{15 c^{3} h^{3}} T^{4}

L'émission spécifique $M$ donnée en W/m² d'un corps noir, par exemple la puissance radiative sortant de l'ouverture d'un radiateur à cavité, est dans la plupart des cas plus significative pour une application pratique que la densité d'énergie en (Ws)/m³ resp. J/m³ à l'intérieur de la cavité. La relation est la suivante :

M = \frac{c}{4} U

Le résultat est la loi de Stefan-Boltzmann :

M = \frac{2 π^{5} k^{4}}{15 c^{2} h^{3}} T^{4} = σ T^{4}

Équations ↓

Avec $h = 6, 6 \cdot 10^{- 34} Js$ , $k = 1, 38 \cdot 10^{- 23} J/K$ et $c = 3 \cdot 10^{8} m/s$ on obtient la constante de Stefan-Boltzmann :

σ = 5.670 \cdot 10^{- 8} \frac{W}{m^{2} K^{4}}

Par conséquent, le rayonnement augmente de manière disproportionnée avec la quatrième puissance de la température. En doublant la température, par exemple de 300 K (température ambiante) à 600 K (327°C, point de fusion de l'aplomb), le rayonnement est multiplié par 16 !

Rayonnement total, 2000 - 7000 K Rayonnement total, 0 - 2200 K

Rayonnement total

M

des corps noirs. À gauche : en MW/m² à des températures comprises entre 2000 et 7000 K. La surface solaire rayonnante a une température d'environ 5800 K. À droite : en kW/m² à des températures comprises entre 0 et 2200 K. 300 K correspond approximativement à la température ambiante.
Source: Rainer Reuter, Université d'Oldenburg, Allemagne.

Le spectre de la Terre

2. Rayonnement thermique

Le rôle de la température : la loi de Stefan-Boltzmann