Supplément 2.4: Loi de déplacement de Wien

Représentation de la longueur d'onde

La distribution de la densité spectrale d'énergie du champ de rayonnement d'un corps noir est :

La longueur d'onde ${\lambda }_{max}$ au maximum de la courbe de rayonnement de Planck sur la température peut être calculée à partir de sa dérivée en l'égalisant avec zéro (problème de l'extrema). Pour une vue d'ensemble claire, nous fixons

Avec la nouvelle variable, la loi de radiation devient :

A l'aide de la règle du quotient, la dérivée sera :

En égalisant avec zéro et en réduisant, on peut trouver une équation transcendante pour l'extremum $x\text{'}$ :

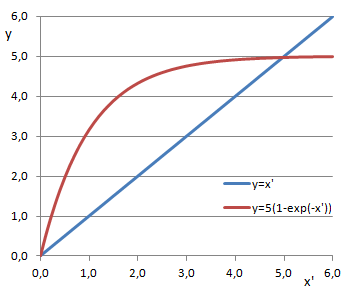
Comme la plupart des équations transcendantes et contrairement aux équations algébriques, elle ne peut être résolue de manière exacte, mais seulement de manière approximative.

Comment trouver la solution ? ↓ ↑

Tout d'abord, nous formons l'équation comme suivant :

$x\text{'}=5\left(1-e^{-x\text{'}}\right)$

Dans un graphique, les côtés gauche et droit sont tracés en fonction de $x\text{'}$. L'intersection des deux courbes indique la valeur de $x\text{'}$ recherchée. Elle est d'environ 5.

Les côtés gauche et droit de l'équation transcendante sont représentés séparément, l'intersection commune étant la solution recherchée.
Source: Rainer Reuter, Université d'Oldenburg, Allemagne

Plus précisément, $x\text{'}$ peut être déterminé de manière itérative. Pour ce faire, on considère des séquences numériques de $x{\text{'}}_{n+1}$ qui résultent des valeurs précédentes de $x{\text{'}}_n$ dans le but de rapprocher continuellement les côtés gauche et droit de la relation

$x{\text{'}}_{n+1}\approx 5\left(1-e^{-x{\text{'}}_n}\right)$.

De cette manière, la valeur réelle peut être déterminée avec un certain degré de précision : $\underset{n\to \infty }{lim}x{\text{'}}_n\to x{\text{'}}_{true}$.

On trouve :

Avec $h=6,6\cdot {10}^{-34}\text{Js}$, $k=1,38\cdot {10}^{-23}\text{J<mo>/</mo>K}$ et $c=3\cdot {10}^8\text{m<mo>/</mo>s}$ il suit la loi de déplacement de Wien :

Représentation des fréquences

Dans ce cas, il n'est pas non plus possible de déduire le maximum $f_{max}$ u maximum de la représentation de la longueur d'onde à gauche ${\lambda }_{\text{max}}$ avec la relation $f\lambda =c$. Les graphiques des courbes de Planck dans les représentations en longueur d'onde et en fréquence montrent que leurs maxima de $f\lambda =c$ ne correspondent pas.

Le calcul doit donc, dans ce cas également, émaner de la loi de rayonnement de Planck sous la forme d'une représentation de la fréquence. Le processus de calcul est comparable à celui illustré dans la colonne de gauche. Les équations correspondantes sont données ci-dessous par souci d'exhaustivité.

La densité spectrale d'énergie du corps noir en fonction de la fréquence est :

La loi de rayonnement avec la nouvelle variable $hf/kT=x$:

Différenciation par rapport à la fréquence :

L'équation transcendante pour le calcul de l'extremum $x\text{'}$

avec la solution $x\text{'}=h{f}_{max}/kT\simeq 2,\mathrm{821...}$.

La loi de déplacement de Wien devient donc :