2. Rayonnement thermique

La lumière comme particule : Loi de Planck     (1/2)

Max Planck a travaillé théoriquement sur le rayonnement dans des cavités isolées, comme mentionné dans les pages précédentes. Celles-ci sont en équilibre thermique et ont des parois idéalement absorbantes. Si l'on éclaire l'intérieur avec une lampe par une petite ouverture, toute la lumière est absorbée par les parois intérieures, de sorte qu'aucune lumière ne sort par l'ouverture. L'espace intérieur est donc un corps noir. En raison de cette caractéristique, on parle également d'émetteur à corps noir ou de radiateur à cavité.

À partir de 1890, la lumière sortante de la cavité a été examinée expérimentalement dans le Lichttechnisches Labor de la Physikalisch-Technische Reichsanstalt à Berlin, ce qui a permis à Planck de bénéficier de données expérimentales très précises.

Rayonnement en fonction de la fréquence

Planck s'est particulièrement intéressé à la densité d'énergie $U$ du rayonnement de la cavité, qui a déjà été mentionnée dans le supplement 1.4; elle décrit l'énergie radiative dans un volume et est donnée en unités de J/m³ ou (Ws)/m³. Ici, c'est la dépendance spectrale de la densité d'énergie qui nous intéresse et nous l'écrivons en fonction de la fréquence :

L'équation de la densité spectrale d'énergie trouvée par Planck en 1900 et qui correspond bien aux données mesurées est la suivante:

avec la constante de Planck $h$, la vitesse de la lumière $c$ et la constante de Boltzmann $k=138\cdot {10}^{-23}\text{ J<mo>/</mo>K}$. Pour trouver cette équation, il a dû supposer que la lumière, c'est-à-dire les ondes électromagnétiques, est constituée de quanta, appelés par la suite photons. L'énergie de ces quanta devrait être donnée par $E=hf$. Le calcul de Planck est décrit dans le supplement 2.2.

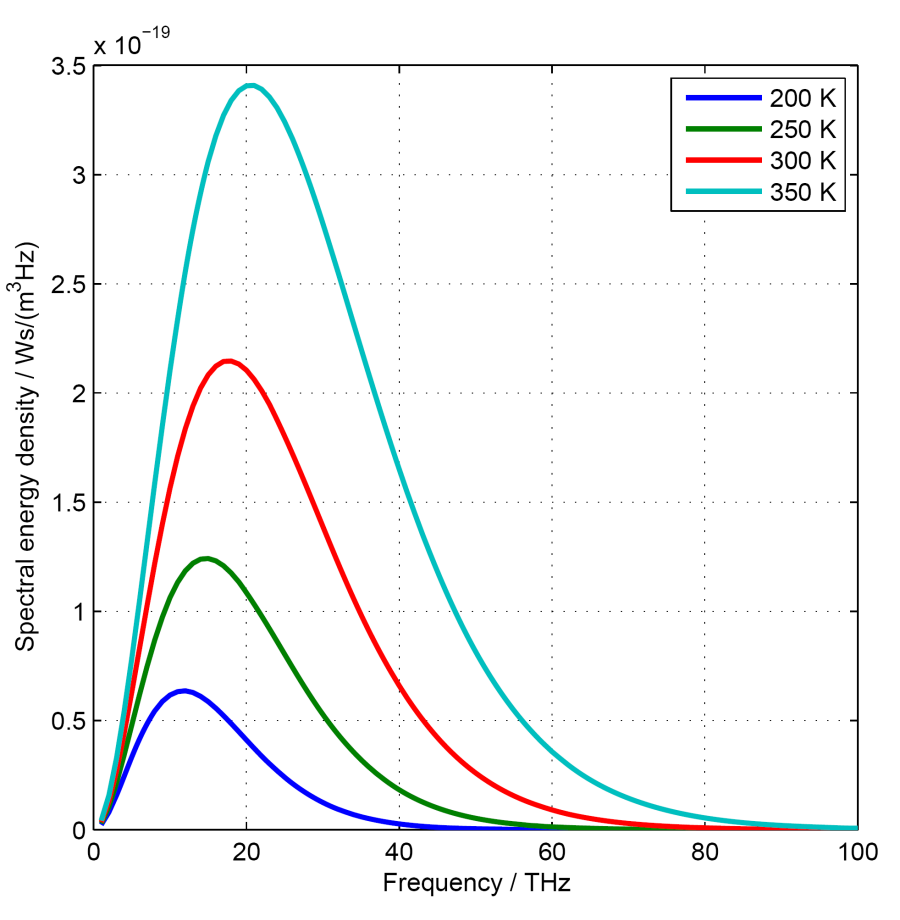
Des exemples de courbes de densité spectrale d'énergie pour des corps noirs sont présentés dans l'image de droite. Elles sont calculées pour des températures comprises entre 200 et 7000 K (correspondant à environ -70° et +6730° Celsius).

D'autres quantités, notamment les propriétés matérielles de l'émetteur, ne jouent aucun rôle. Il peut s'agir d'un objet solide, d'un liquide ou d'un gaz.

La quantité de chaleur emmagasinée dans un corps noir n'est pas non plus pertinente. Ceci est mis en évidence par le degré d'absorption $\alpha =1$: seule la couche superficielle opaque du corps émet, car la matière interne absorbe entièrement le rayonnement.

Afin de mieux reconnaître les températures dans les graphiques :

• la température ambiante est d'environ 300 K
• la température de la chaleur rouge est d'environ 1500 K
• le soleil émet à des températures de surface d'environ 6000 K

200-400 K 400-1000 K 1000-2500 K 2500-4000 K 4000-7000 K

Graphiques d'émission des corps noirs en fonction de la fréquence à différentes températures en Kelvin.

Troisième propriété remarquable du rayonnement du corps noir : les courbes d'émission de corps ayant des températures différentes ne se croisent pas. Au contraire, l'émission d'un émetteur chaud est plus élevée à toutes les fréquences ou longueurs d'onde que l'émission d'un émetteur plus froid.