Supplément 2.2: Loi de Planck sur le rayonnement    (1/2)

Max Planck a imaginé le concept de cavité : Son rayonnement est en équilibre thermique avec la surface de l'espace interne. Les atomes de la surface absorbent tout le rayonnement entrant. Pendant ce temps, ils émettent des ondes électromagnétiques obéissant à la loi du rayonnement de Kirchhoff avec le plus haut degré d'émission $\epsilon =1$ possible pour les corps noirs.

Une deuxième réflexion conceptuelle concerne l'énergie des ondes émises par les atomes de la surface. Ces ondes sont liées aux atomes oscillants, appelés oscillateurs. Selon la physique classique, ces valeurs d'énergie sont distribuées de manière continue : L'énergie d'oscillation dans un système oscillant classique peut prendre des valeurs distribuées de manière continue. Planck supposait cependant que ces énergies étaient quantifiées. Par conséquent, elles ne peuvent prendre que des valeurs discrètes. Cela contredisait la physique classique, mais conduisait à la bonne conclusion et représente donc la base d'un nouveau développement, la théorie quantique.

Ondes dans une cavité

Nous observons une petite partie du spectre à une fréquence $f$ et la densité d'énergie actuelle $\text{d}U=u_f\text{d}f$ des ondes dans un intervalle de fréquence infinitésimal $\text{d}f$. Elle semble pouvoir être exprimée par la densité d'énergie midspectrale d'une seule onde, multipliée par les ondes existantes dans l'intervalle $\text{d}f$.

Le nombre de ces ondes peut être estimé. Conformément à la théorie de Maxwell sur les ondes électromagnétiques, l'intensité du champ électrique doit être nulle à la surface. C'est là que seules des ondes stationnaires avec des nœuds d'oscillation peuvent apparaître, si leur longueur d'onde dans une cavité de l'étendue intérieure $L$ est qualifiée de :

Se poursuit : $n=\mathrm{0<mo>,</mo>}\mathrm{1<mo>,</mo>}\mathrm{2<mo>,</mo>}\mathrm{3<mo>,</mo>}\mathrm{...}$ Seuls des multiples entiers de la longueur d'onde bissectée s'adaptent à la distance $L$, si un nœud est supposé apparaître sur les bords. Les longueurs d'onde possibles ne sont donc pas continues mais discrètement distribuées ; elles forment les oscillations intrinsèques, appelées modes, de la cavité.

Les nombres d'onde et les fréquences correspondent donc à :

En reformulant la dernière relation et en la différenciant, pour le nombre requis de modes d'oscillation dans l'intervalle de fréquence, on obtient ce qui suit :

Il faut maintenant tenir compte de la tridimensionnalité de la cavité, c'est-à-dire des caractéristiques des ondes qui oscillent dans les trois dimensions x, y et z. Il en résulte des valeurs de nombres discrets n_x, n_y et n_z pour ces directions de coordonnées. Combien d'ondes $\text{d}N$ sont présentes dans le vide au total ?

Pour ce faire, nous examinons les ondes dans un espace tridimensionnel dont les coordonnées sont n_x, n_y et n_z. Les ondes correspondant à l'intervalle de fréquence $\text{d}f$ se trouvent dans une coque sphérique de cet espace avec le rayon

et l'épaisseur $\text{d}n$. Leur volume résulte de la multiplication de la surface de la sphère par l'épaisseur de la coquille $4\pi n^2\text{d}n$.

Des valeurs exclusivement positives pour n_x, n_y et n_z sont légitimes (les longueurs d'onde dans les conditions d'ondes stationnaires sont positives). Dans un seul des huit octants du système de coordonnées, toutes les valeurs sont positives. C'est donc la seule autorisée.

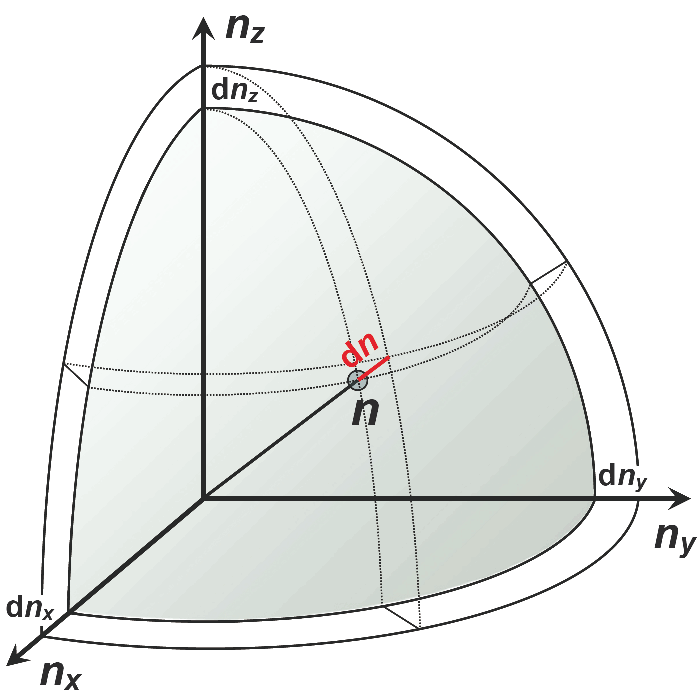
Espace tridimensionnel des modes d'oscillation possibles des ondes stationnaires dans une cavité. Seul l'octant avec des valeurs exclusivement positives est représenté.

Chaque onde peut apparaître avec deux polarisations orthogonales, ce qui doit être pris en compte par le facteur 2. On obtient ainsi le nombre d'états d'oscillation en appliquant les expressions arithmétiques pour $n$ et $\text{d}n$:

Ce faisant, sans limitation de la généralité, on suppose que la cavité a la même expansion $L$ dans les trois dimensions. Avec le volume $V=L^3$, on obtient le nombre de modes du vide dans l'intervalle de fréquence $\text{d}f$: