2. Introduction aux méthodes mathématiques

Mesure de valeurs

Parfois, vous voudrez représenter toutes vos données par une seule valeur. Laquelle vaut-il mieux utiliser ?

Il y a trois valeurs principales que vous pouvez utiliser :

  • La moyenne
  • Le mode
  • La médiane

Pour un ensemble d'observations donné, tel { x 1 , x 2 , x 3 , …, x i , …, x n } où chaque x i est une observation individuelle, alors la moyenne est donnée par la formule :

X ¯ = ( x 1 + x 2 + x 3 +...+ x n ) n = ∑ i=1 n x i n

Remarquez que la moyenne de l'échantillon est représentée par le symbole x ¯ appelé x barre. Cette équation représente la somme des n observation individuelles divisées par le nombre (n) d'observations. Le symbole utilisé pour une somme d'observation est la lettre grecque Σ (sigma). La lettre sous le sigma indique le paramètre de la somme qui va changer (celui qui sera sommé), i dans la suite { x 1 , x 2 , x 3 , …, x i , …, x n } . Les valeurs sous et sur sigma indiquent la première et dernière valeur données à ce paramètre, ainsi :

∑ i = 1 4 x i  =  x 1  +  x 2  +  x 3  +  x 4

Lorsque vos données sont une distribution de fréquences, chaque classe de la distribution de fréquences donne le nombre d'occurrence d'une valeur, ou le nombre d'observations dans cette classe. Sachant cela, la moyenne est calculée comme la somme des produits des valeurs des classes par le total de classes et divisé par la somme des totaux de chaque classe.

Donc, pour des données groupées :

x ¯  =  ∑ k i · v i ∑ k i

Où k i et v i sont respectivement le compte (total) et la valeur de la classe i de l'histogramme.

La mode est la valeur qui apparait le plus fréquemment dans un jeux de données, et la médiane est la séparation entre la moitié supérieure et la moitié inférieure de l'échantillon. C'est la valeur médiane, entre la plus grande et la plus basse valeur du jeu de données. Si il y a un nombre pair de données dans l'échantillon, comme c'est le cas, par exemple, pour un dé, alors la médiane est le " milieu " des données, c'est-à-dire 3,5 pour un dé.




Exemple : Voici un jeu de données, résultat de lancés de dés :
1, 3, 5, 2, 4, 4, 1, 6, 1

Le mode de ce jeu de donnée est 1, car cette valeur apparait trois fois, alors que les autres valeurs possible n'apparaissent que une ou deux fois.

La médiane de ces données est 1+62=3,5.

La moyenne de ces données est X=1+3+5+2+4+4+1+6+19=279=3.

Zoom Sign
Sample distribution
Distribution d'un échantillon

Questions

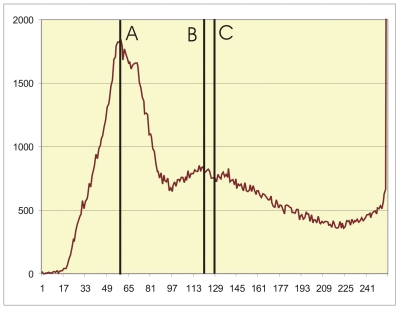
  1. Dans l'histogramme ci-dessus, la moyenne, médiane et mode sont tous représentés comme des lignes, avec les symboles A, B et C. Quelle ligne représente quelle valeur ??

  2. Nous avons parlé de la moyenne de l'échantillon, x ¯ . Quelle est la moyenne de la population, µ, et la moyenne de la population varie-t-elle de la moyenne de l'échantillon, si oui, pourquoi ? Indice : lisez les définitions d'échantillon et de population dans le Glossaire.

Exercices, tutoriaux et réponses