Geostrofische stromen

Van oppervlaktehelling tot stroomsnelheid

Je zult je afvragen hoe een oceanograaf metingen van de oppervlaktehelling omzet in een maat van de stroomsnelheid. De basisaanname is dat wanneer we naar de grote stromen kijken op schalen van 100 km of meer, er een wezenlijk evenwicht is tussen twee krachten - de drukgradiënt en de Coriolis-kracht die je in hoofdstuk 2 gezien hebt.

Kijk naar onderstaande figuur om dit te begrijpen.

Stel je even voor dat er een "hoog" en een "laag" is in de zeeoppervlakte (een altimeter kan deze meten!) en dat er geen Corioliseffect is. Water zou natuurlijk van hoog naar laag stromen om het evenwicht te herstellen. Met andere woorden, er is een kracht die het water van het hoge niveau naar het lage niveau duwt - en deze kracht is proportioneel aan het verschil in niveaus, d.w.z. de "drukgradiënt".

Maar denk er nu aan dat in de echte wereld de Corioliskracht er WEL is - en deze zal de kracht naar rechts trekken op het noordelijk halfrond (zoals je in onderstaande figuur kunt zien) en naar links op het zuidelijk halfrond.

Het evenwicht tussen drukgradiëntkrachten en Corioliskrachten op een deeltje water is wat wij het geostrofisch evenwicht noemen.

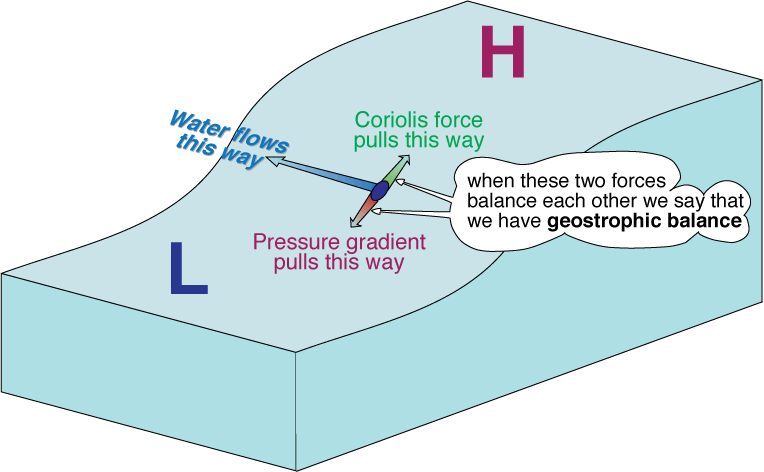
Wanneer de situatie is zoals voorgesteld in bovenstaande figuur, zeggen we dat er een geostrofisch evenwicht is en dat de stroom zuiver geostrofisch is. Het mooie daarvan is dat de stroom vlot uit de meting van de helling berekend kan worden.

In feite wordt de Corioliskracht gegeven door de stroomsnelheid v maal een parameter f, de Coriolisparameter genoemd (de Coriolisparameter varieert met de breedtegraad: op 45° is de waarde ervan ongeveer 10^-4 s^-1), terwijl de drukgradiënt de helling dh/dxis (waar h de hoogte is en x de afstand) maal g, de zwaartekrachtversnelling (9,81 m s^-2).

Dus als we gewoon het geostrofisch evenwicht schrijven, d.w.z. we schrijven

kunnen we onmiddellijk vberekenen als

en de richting van de stroom zal loodrecht op de helling zijn, zoals getoond in de figuur.

Voorbeelden van twee verschillende zeeoppervlaktehellingen die overeenstemmen met verschillende oppervlaktestromen volgens de geostrofie.

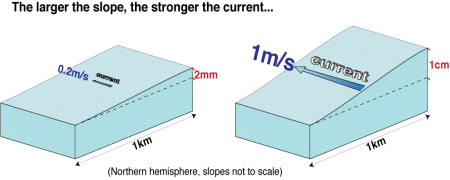
Niet alle stromen zijn geostrofisch

De aanname dat er geostrofisch evenwicht is, is maar nauwkeurig wanneer we naar stromen op grote schaal kijken, d.w.z. op schalen groter dan een paar tientallen km. Alle grote stromen kunnen geostrofisch beschouwd worden bij een eerste benadering. Op kleinere schalen worden de a-geostrofische (niet geostrofische) componenten van de stromen steeds belangrijker, bijvoorbeeld vanwege de stuwing van de lokale wind,. Dus bijvoorbeeld in verschillende kustgebieden is de circulatie in ruime mate a-geostrofisch. Een altimeter kan echter nog steeds gebruikt worden om de geostrofische component te meten.