Φύλλο Εργασίας Η Θαλάσσια Ρύπανση c02-02-4 - Οδηγίες για τους εκπαιδευτικούς

Σενάριο

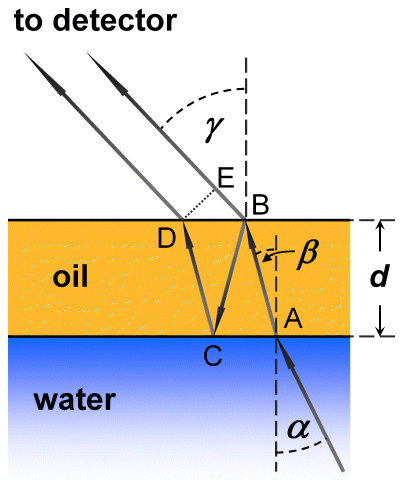
Θέλουμε να έχουμε μια βαθύτερη κατανόηση των παρυφών παρεμβολών που παρατηρούνται στην μικροκυματική ραδιομετρία. Στο γράφημα, η γεωμετρική διαφορά της πορείας των ακτίνων Δs των κυμάτων είναι: $\Delta s=n_{oil}\left(\overline{BC}+\overline{CD}\right)-\overline{BE}$ Χρησιμοποιώντας τριγωνομετρικές σχέσεις και το νόμο του Snell, αυτό γίνεται: $\Delta s=2d\sqrt{n_{oil}^2-{sin}^2\gamma }$ Λόγω αυτής της γεωμετρικής διαφοράς πορείας, υπάρχει μια διαφορά φάσης $\Delta \varphi$ των κυμάτων: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s$ Στο σημείο C, ο κύμα υφίσταται μια αντανάκλαση σε ένα μέσο με μεγαλύτερο δείκτη διάθλασης (δηλαδή, το νερό). Ως εκ τούτου, υπάρχει άλμα της φάσης του π του ανακλώμενου κύματος. Η διαφορά της φάσης των κυμάτων γίνεται: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s-\pi$ όπου ο όρος -π είναι από το άλμα της φάσης στο σημείο C. Υπάρχει εποικοδομητική παρέμβαση με $\Delta \varphi =\pi m$ και καταστροφική παρέμβαση με $\Delta \varphi =\pi (2m+1)$, όπου το m είναι ένας ακέραιος αριθμός..

Ένα στρώμα πετρελαίου με πάχος d στην επιφάνεια του νερού, και τα μικροκύματα με την πορεία ακτίνων κατευθύνονται προς τον ανιχνευτή του μικροκυματικού ραδιομέτρου.

Ασκήσεις

Αύτα μπορούν να κάνουν οι μαθητές (Συνεχίζεται από το Φύλλο Εργασίας Η Θαλάσσια Ρύπανση C02-03):

7. Χρησιμοποιώντας τριγωνομετρικές σχέσεις και το νόμο του Snell, αποδείξετε ότι η διαφορά της γεωμετρικής πορείας Δs των κυμάτων κατέχει όπως αναφέρεται παραπάνω, ανάλογα με το πάχος του στρώματος του πετρελαίου d, ο δείκτης διάθλασης του πετρελαίου n, και η γωνία συχνότητας α. .
8. Παρακαλούμε να υπολογίσετε τη διαφορά φάσης των κυμάτων για ένα στρώμα πετρελαιού με πάχος από 0 έως 5μμ με βήματα των 0,25μμ με τα ακόλουθα στοιχεία: f = 34 GHz, noil = 1,41, γ = 50 °. Να λάβετε υπόψη σας το άλμα της φάσης του κύματος που αντανακλώνται στο σημείο C. Επιβεβαιώστε την ορθότητα της θέσης του μέγιστου και ελάχιστου της καμπύλης θερμοκρασίας φωτεινότητας που αναφέρεται στη σελίδα 2 του συμπληρώματος για τα μικροκυματικά ραδιόμετρα.

Λύσεις

7. Οι αποστάσεις $\overline{AB}$, $\overline{BC}$, και $\overline{CD}$ έιναι ίδιες. Δηλαδή:                         $n_{oil}\left(\overline{BC}+\overline{CD}\right)=\frac{2n_{oil}d}{cos\beta }$

   Οι ακόλουθες σχέσεις παραμένουν:                                        $sin\gamma =\frac{\overline{BE}}{\overline{BD}}tan\beta =\frac{\overline{BD}}{2d}tan\beta =\frac{sin\beta }{cos\beta }$

   Με $sin\gamma /sin\beta =n_{oil}$ αποκτάμε:                         $\Delta s=\frac{2nd}{cos\beta }-\frac{2nd{sin}^2\beta }{cos\beta }=2ndcos\beta =2d\sqrt{n_{oil}^2-{sin}^2\gamma }$

Υλικά

• Έκδοση του πρόσθετου φύλλου εργασίας: Παρυφές παρεμβολών του λαδιού στο νερό, ως σελίδα html ή ως μορφή για εκτύπωση rtf
• Η πετρελαϊκή ρύπανση και η τύχη του πετρελαίου στη θάλασσα
• Αερομεταφερόμενη θαλάσσια επιτήρηση πετρελαιοκηλίδων
• Το ραδιόμετρο μικροκυμάτων

Απαιτούμενος χρόνος

• Δυο σχολικές ώρες και δυο ασκήσεις για το σπίτι
  
  

Διαδικασία

• Αυτές οι ασκήσεις μπορούν να χρησιμοποιηθούν ως εργασία στο σπίτι στο μάθημα της φυσικής, μετά από συζήτηση του φύλλου εργασίας Η Θαλάσσια Ρύπανση C02-02-3 μέσα στην τάξη.

Ιστορικό

• Εγχειρίδια για την οπτική - το θέμα είναι ίδιο με την παρέμβαση των κυμάτων φωτός οι οποίες διαβιβάζονται μέσω (ή: αντανακλούνται από) μια λεπτή επίπεδη παράλληλη γυάλινη πλάκα