Werkblad Mariene Vervuiling c02-02-4

Scenario

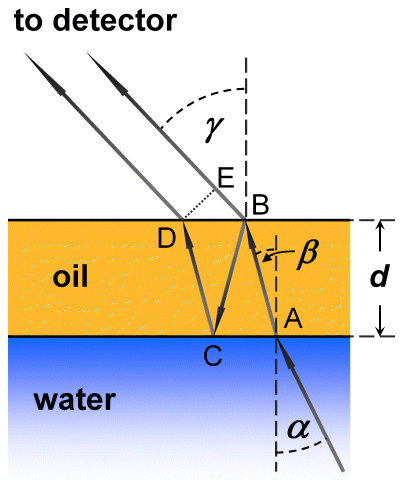
We willen een dieper inzicht verkrijgen in de interferentieranden die met microgolfradiometrie waargenomen worden. In de tekening is het geometrisch verschil van de straalbanen Δs van de golven: $\Delta s=n_{olie}\left(\overline{BC}+\overline{CD}\right)-\overline{BE}$ Met behulp van trigonometrische relaties en de Wet van Snell wordt dit: $\Delta s=2d\sqrt{n_{olie}^2-{sin}^2\gamma }$ Door dit verschil in geometrische baan is er een faseverschil $\Delta \varphi$ van de golven: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s$ Bij punt C ondergaat de golf een weerkaatsing bij een medium met een hogere brekingsindex (bv. het water). Dus er is een fasesprong van π van de weerkaatste golf. Het faseverschil van de golven wordt: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s-\pi$ waar de term -π komt van de fasesprong bij punt C. Er is constructieve interferentie bij $\Delta \varphi =\pi m$ en destructieve interferentie bij $\Delta \varphi =\pi (2m+1)$, waar m een geheel getal is.

Een olielaag met dikte d op het wateroppervlak en microgolven met een stralenbaan gericht naar de detector van de microgolfradiometer.

Oefeningen

Dit is wat studenten kunnen doen (vervolg van werkblad Mariene vervuiling C02-03):

7. Toon met behulp van trigonometrische relaties en de Wet van Snell aan dat het verschil van het geometrisch pad Δs van de golven geldt zoals hiervoor opgegeven, afhankelijk van de olielaagdikte d, de brekingsindex n van de olie en de invalshoek α.
8. Bereken a.u.b. het faseverschil van golven voor een olielaagdikte van 0 tot 5 mm in stappen van 0,25 mm met de volgende gegevens: f=34 GHz, n_olie=1,41, γ=50°. Houd ook rekening met de fasesprong van de bij punt C weerkaatste golf. Controleer of de positie van de maxima en minima van de helderheidstemperatuurcurve correct is, zoals te zien is op pagina 2 van het bijvoegsel over microgolfradiometers.

Materialen

• Studentenversie van dit bijgevoegd werkblad: Interferentieranden van olie op water, als afdrukbaar rtf-bestand
• Olievervuiling en het lot van olie op zee
• Maritieme olievlekbewaking vanuit de lucht
• De microgolfradiometer

Achtergrondinformatie

• Leerboeken over optica; het onderwerp is identiek aan de interferentie van lichtgolven die doorgezonden (of: weerkaatst) worden door een dunne, vlakke evenwijdige glasplaat.