Messprinzip
Geometrie des SLAR-Messverfahrens und geometrische Auflösung am Boden. Die SLAR-Antenne (rot hervorgehoben) hat die Länge
und ist an der Unterseite des Flugzeugs montiert. Seine Flughöhe ist H. Wir betrachten einen Ausschnitt des Strahls,
der unter dem Nadirwinkel θ emittiert wird. Das rot markierte Element bezeichnet ein im Abstand R bestrahltes Volumen.
Die weiteren Größen sind im Text genannt.
Eine weitere Eigenschaft von Radar-Geräten ist die Polarisation der ausgesandten Radar-Pulse und empfangenen Signale.
Wegen der langgestreckten Form der SLAR-Antenne und der Anordnung ihrer Längsachse in Flugrichtung werden elektromagnetische Wellen
abgestrahlt, deren elektrischer Feldvektor - bezogen auf die Einfallsebene des Fächerstrahls am Boden - senkrecht ausgerichtet ist.
Aus dem selben Grund werden rückgestreute Wellen mit gleicher Orientierung ihres elektrischen Feldvektors empfangen.
Dies wird als VV-Polarisation bezeichnet, d.h. vertikal hinsichtlich der abgestrahlten und empfangenen Wellen. Andere Geräte, z.B.
Radar-Geräte auf Satelliten im Weltraum können für spezielle Anwendungen auch eine HH-Polarisation (horizontal-horizontal)
und eine HV- oder VH-Polarisation (also eine gekreuzte Polarisation der ausgesandten und empfangenen Wellen) nutzen.
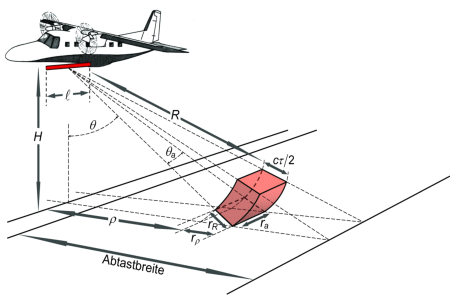
Die Größe der Bildelemente - die als Pixel bezeichnet werden - hängt von der Breite des Fächerstrahls in Flugrichtung
und der Pulslänge in Richtung des Abstands R ab. Für den horizontalen Antennenöffnungswinkel θa
ergibt sich aus der Theorie der Beugung elektromagnetischer Wellen:
wobei λ die Wellenlänge des Radars und
die Antennenlänge bedeuten.
Synthetische Antennen ↓ ↑
Die Antennenlänge ist offensichtlich
für den horizontalen Öffnungswinkel θa und somit für die geometrische Auflösung
am Boden ein ganz wesentlicher Parameter: je länger die Antenne, desto kleiner ist dieser Winkel. Dies ist
besonders wichtig für Instrumente auf Satelliten, da andernfalls die sehr viel größere Entfernung
zur Erdoberfläche eine sehr schlechte Bodenauflösung ergäbe.
Der Nachteil einer kurzen Antenne lässt sich beheben, wenn man sie künstlich bis zu den gewünschten Abmessungen
vergrößert. Wegen der Kohärenz der Radar-Signale ist dies tatsächlich möglich! Wir nehmen an, ein Objekt wird nacheinander von mehreren Pulsen
bestrahlt und das Flugzeug oder der Satellit registriert die Pulsantworten entsprechend nacheinander während des Überflugs.
Werden diese Empfangssignale gespeichert, so können sie ausgewertet werden als wären sie gleichzeitig von einer Antenne
empfangen worden, deren Länge der Flugstrecke entspricht, die zwischen dem ersten und dem letzten Puls zurückgelegt wurde.
Hiermit ist es möglich, Objekte am Boden längs der Flugrichtung geometrisch aufzulösen, die in ihren Abmessungen den
der Länge ungefähr der synthetisch vergrößerten Antennnenlänge entsprechen.
Solche Radar-Geräte werden als Radar mit Synthetischer Apertur oder SAR
(englisch: Synthetic Aperture Radar) bezeichnet. Eine detailliertere Darstellung findet sich
in einem Abschnitt über das Satelliten-SAR.
Radar-Geräte mit einer Antenne, wie sie im vorliegenden Abschnitt beschrieben ist, werden als Radar mit realer Apertur oder
RAR bezeichnet. Das in der Meeresüberwachung genutzte Seitensichtradar (SLAR) ist ein RAR.
Die Auflösung in Flugrichtung ist daher:
Sie ist demnach eine Funktion des Abstands R und in verschiedenen Bereichen eines Radar-Bilds unterschiedlich groß.
Die Auflösung querab zur Flugrichtung ist:
wobei τ die Pulslänge des Radar, c die Lichtgeschwindigkeit
und θ der Nadirwinkel des betrachteten Teilstrahls ist. Der Faktor 2 im Nenner
erklärt sich durch den Hin- und Rückweg des Strahls über die Strecke rR.
Die Horizontalauflösung am Boden wird dann:
Die Pixelabmessungen ra und rρ hängen vom Einfallswinkel
θ and daher auch von der Entfernung zum Objekt querab des Flugkurses ab.
Aufgabe: Radar-Pixelgröße
↓ ↑
Wir sind unterwegs auf einem Überwachungsflug vor der Küste. Unser SLAR hat die folgenden Daten:
- Antennenlänge: 3 m
- Mikrowellenfrequenz: 10 GHz
- Pulslänge: 50 ns
- horizontaler Antennenöffnungswinkel: 0,5°
Die Flughöhe ist 1000 m. In einer horizontalen Entfernung von 5 km querab zum Flugkurs
sehen wir ein Objekt im Radar-Bild. Könnte dieses Objekt (a) ein etwa 1 m kleines Fass sein,
oder eher (b> ein verloren gegangener 30 Fuß-Container, oder (c) vielleicht sogar ein 50 m langes Schiff?
