Ergänzung 3.2: Ebene Winkel und Raumwinkel (2/2)

Raumwinkel

Räumliche Winkel kommen durch die Erweiterung des Konzepts ebener Winkel in den dreidimensionalen Raum zustande. Aus dem Kreis (2D) wird eine Kugel (3D); aus der Länge eines Kreisbogens (2D) wird die Fläche auf einer Kugel (3D). Der Raumwinkel Ω, siehe Abbildung unten, definiert sich entsprechend als Verhältnis einer Kugelsegmentfläche a zum Quadrat des Kugelradius R:

Ω = \frac{a}{R^{2}}

Ein Raumwinkel Ω in einer Halbkugel. Er ist gleich dem Verhältnis von Kugelsegmentfläche a zum Quadrat des Kugelradius R. Die Kugelsegmentfläche ist mit einem Kreis als Randlinie dargestellt; es gibt jedoch keine Einschränkung der Form von Raumwinkeln.

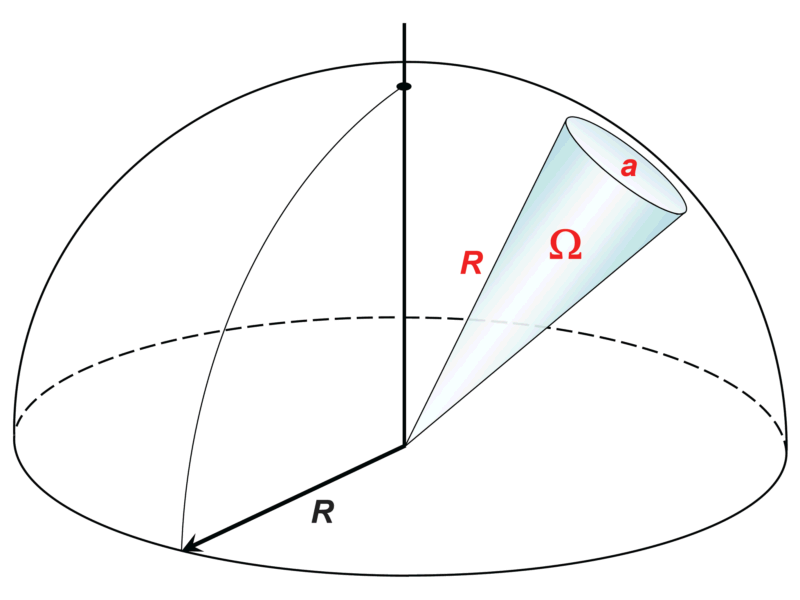
Man benennt Raumwinkelwerte mit der dimensionslosen Einheit Steradiant, mit dem Zeichen sr. Angaben in Grad wie bei ebenen Winkeln gibt es nicht.

Aufgabe: Raumwinkel ↓

Berechnen Sie bitte mit der Gleichung der Oberfläche einer Kugel die Raumwinkel, die sich aus folgenden Größen der Kugelsegmentfläche a ergibt:
a) Fläche einer Halbkugel (der Halbraum, siehe Grafik oben)
b) Fläche einer Kugel (der Raum)

Der Raumwinkel des Halbraums ist zum Beispiel durch das Firmament von Horizont zu Horizont gegeben (im Flachland, wenn keine Berge das Firmament begrenzen).

Die Ergebnisse Ihrer Rechnung sollten sein: a) $2 π$ , b) $4 π$ .

Für kleine Raumwinkel kann eine Kugelsegmentfläche näherungsweise als eben angesehen werden, wodurch sich die Berechnung von Raumwinkeln vereinfacht.

Differenzielle Raumwinkel

So wie ein ebener Winkel als differenzielle Größe angegeben werden kann,

d φ = \frac{d s}{r}

wird auch ein differenzieller Raumwinkel geschrieben:

d Ω = \frac{d a}{R^{2}}

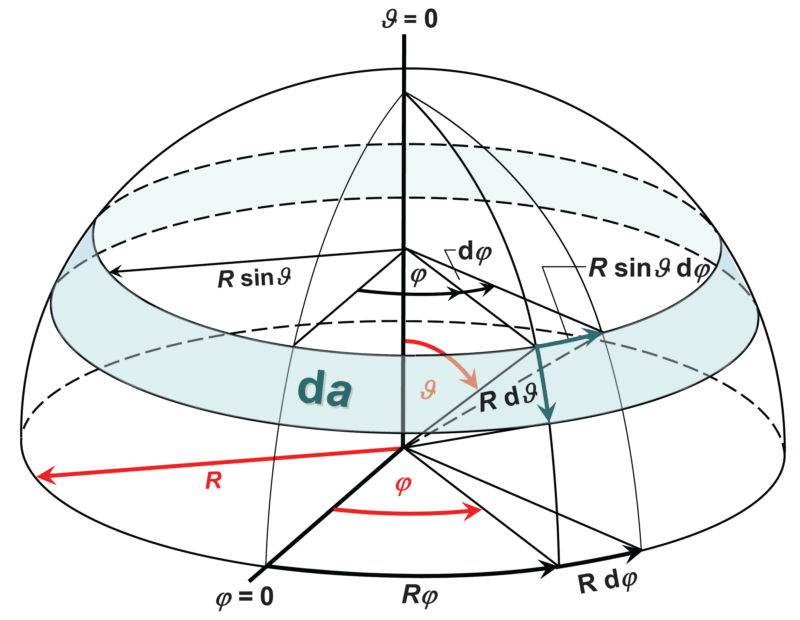
Die Orientierung eines Raumwinkelelements im Raum wird übersichtlich durch räumliche Polarkoordinaten (oder: Kugelkoordinaten) festgelegt. Die Abbildung in der rechten Spalte oben zeigt eine differenzielle Kugelsegmentfläche da in Polarkoordinaten (r,ϑ,φ); geteilt durch das Quadrat des Kugelradius R wird daraus ein differenzieller Raumwinkel dΩ.

Ein differenzielles Flächenelement da auf einer Kugeloberfläche. Geteilt durch das Quadrat des Kugelradius R ergibt es das Raumwinkelelement dΩ.

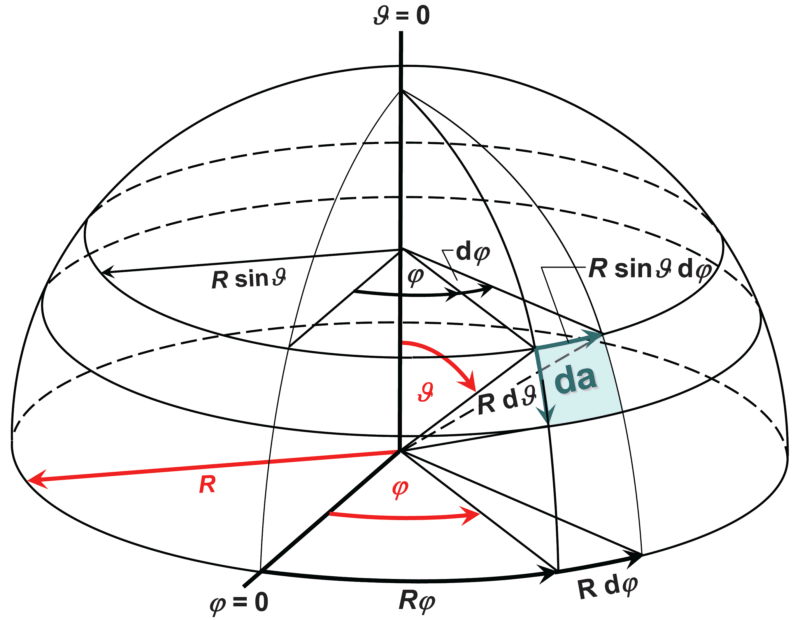
Mit den geometrischen Beziehungen, die für den Rand der als ebenes Rechteck angenommenen differenziellen Fläche da in Polarkoordinaten gelten (siehe Abbildung oben), kann der Raumwinkel folgendermaßen geschrieben werden:

d Ω = \frac{d a}{R^{2}} = \frac{(R sin ϑ d φ) (R d ϑ)}{R^{2}} = sin ϑ d ϑ d φ

Häufig ist ein physikalischer Vorgang nur vom Zenitwinkel ϑ abhängig, während der Azimutwinkel φ keine Rolle spielt. Dann kann die Variable φ in der Gleichung für da durch Integration eliminiert werden:

\int_{φ = 0}^{2 π} (R sin ϑ d φ) (R d ϑ) = R^{2} sin ϑ d ϑ \int_{φ = 0}^{2 π} d φ = 2 π R^{2} sin ϑ d ϑ

Die so entstandene differenzielle Fläche da gleicht einem Band um die Kugel unter dem Zenitwinkel ϑ mit der Breite R dϑ, siehe Abbildung unten.

Ein azimutsymmetrisches differenzielles Flächenelement da auf einer Kugeloberfläche.

Der entsprechende differenzielle Raumwinkel ist:

d Ω = 2 π sin ϑ d ϑ

Aufgabe: Integration des differenziellen Raumwinkels ↓

Integrieren Sie bitte die Gleichung $d Ω = 2 π sin ϑ d ϑ$ über den Zenitwinkel ϑ in den Grenzen
a) 0 und $π / 2$ (oder: 90°)
b) 0 und $π$ (oder: 180°)

Die Ergebnisse Ihrer Rechnung sollten sein: a) $2 π$ , b) $4 π$ , wie in der Aufgabe in der linken Spalte.

Fernerkundung mit Lasern

Ergänzung 3.2: Ebene Winkel und Raumwinkel (2/2)

Raumwinkel

Differenzielle Raumwinkel