Ergänzung 3.1: Polarkoordinaten

Kartesische Koordinaten

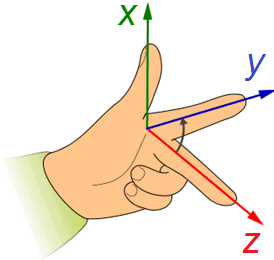
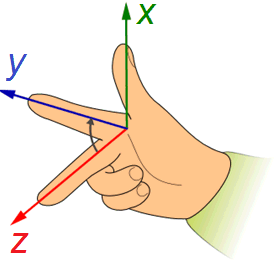
Die Lage von Punkten, Linien oder Flächen in einer Ebene wird meist in kartesischen Koordinaten angegeben. Das ist ein orthogonales Koordinatensystem, in dem die beiden Koordinatenachsen senkrecht aufeinander stehen. Die Variablen x und y sind in einem rechtshändigen System auf der Rechtsachse (der Abszisse) und der Hochachse (der Ordinate) aufgetragen.

In vielen Fällen können physikalische Zusammenhänge mit dem Abstand zum Koordinatenursprung und dem Winkel gegen eine Koordinatenachse einfacher dargestellt werden. Beispielsweise ist die Schwerkraft der Erde auf einen Körper immer zum Erdmittelpunkt gerichtet, also radialsymmetrisch. Nutzt man den Erdmittelpunkt als Ursprung eines Koordinatensystems, dann sind Betrag und Richtung der Schwerkraft, die etwa auf einen Satelliten im Weltraum wirkt, leichter durch den Abstand zum Ursprung und den Winkel gegen die Polachse darstellbar als in kartesischen Koordinaten. Ähnliche Gründe gelten für die Ausbreitung von Licht (auch Laserlicht) und für die Beobachtung von Objekten mit dem Objektiv einer Kamera oder mit einem Teleskop: auch hier liegt eine radiale Symmetrie vor.

Ebene Polarkoordinaten

Ein ebenes Polarkoordinatensystem verwendet die in der unten gezeigten Grafik definierten Variablen (r,φ) zur Bestimmung der Lage von Punkten, Linien oder Flächen.

In kartesischen Koordinaten wird die Lage des Punkts P durch seine (x,y)-Koordinaten angegeben. Polarkoordinaten nutzen den Abstand r zum Ursprung und den Winkel φ mit der x-Achse (rot hervorgehoben); der Punkt wird durch P(r,φ) dargestellt.

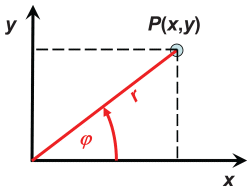
Die Transformationsgleichungen sind:

Räumliche Polarkoordinaten

Ein dreidimensionales kartesisches Koordinatensystem nutzt zusätzlich eine z-Achse, in einem rechtshändigen System orientiert wie in der unten gezeigten Abbildung. In Polarkoordinaten wird entsprechend

• der Abstand r zum Ursprung,
• der Winkel φ gegen die x-Achse (Azimutwinkel), und zusätzlich
• der Winkel ϑ gegen die z-Achse (Zenitwinkel)

genutzt, um die Lage des Punks P zu bestimmen. Räumliche Polar- koordinaten werden auch Kugelkoordinaten genannt.

In kartesischen Koordinaten wird die Lage des Punkts P durch seine (x_p,y_p,z_p)-Koordinaten angegeben (mit dem Index p werden die Koordinatenwerte von P von den Koordinatenachsen unterschieden). Polarkoordinaten nutzen (rot hervorgehoben) den Abstand r zum Ursprung, und die Winkel φ und ϑ; der Punkt wird durch P(r_p,ϑ_p,φ_p) dargestellt.

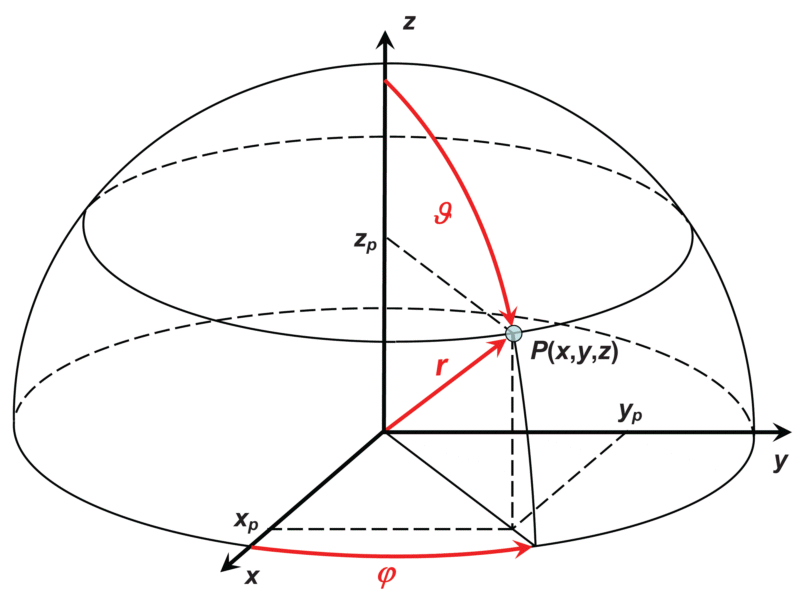
Die Transformationsgleichungen sind:

In Ergänzung 2 werden ebene und räumliche Winkel definiert. Die Geometrie von Instrumenten zur Messung von Licht wird in Ergänzung 3 erklärt.