Ergänzung 3.2: Ebene Winkel und Raumwinkel (1/2)

Ebene Winkel

Der Winkel φ zwischen zwei Geraden, siehe linke Abbildung unten, bestimmt sich aus der Teilung eines Kreises um den Schnittpunkt der Geraden.

Links: Der Winkel φ als Verhältnis von Kreisbogenlänge s zu Radius r. Rechts: Der gleiche Winkel in einem rechtwinkligen Dreieck mit der Gegenkathete a, der Ankathete b und der Hypotenuse r.

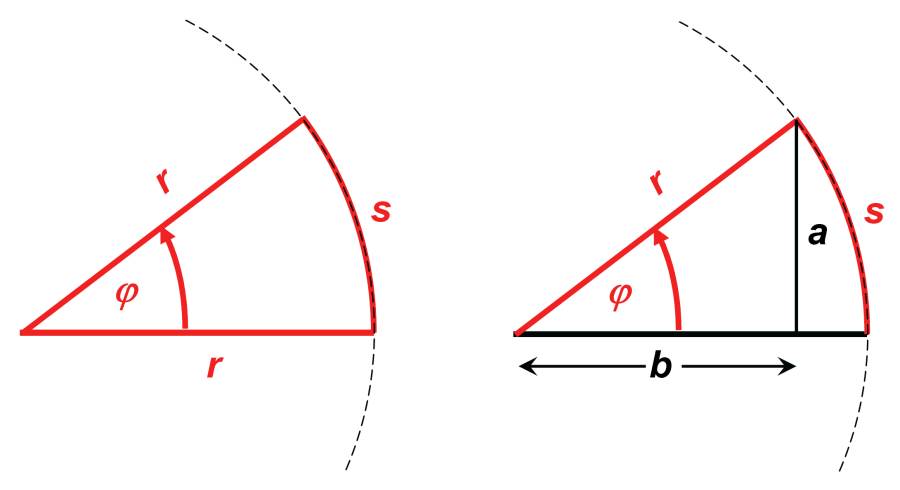
Bogenmaß

Der Quotient aus Kreisbogenlänge s und Radius r kennzeichnet den Winkel φ im Bogenmaß:

Man benennt Winkel im Bogenmaß mit der dimensionslosen Einheit Radiant, mit dem Zeichen rad. Für kleine Winkel ist der Milliradiant mit dem Zeichen mrad gebräuchlich, es ist 1000 mrad=1 rad.

Gradmaß

Teilt man den Kreisumfang in 360 gleiche Teile, so entspricht der Richtungsunterschied zweier Geraden vom Kreismittelpunkt zu zwei benachbarten Teilpunkten auf dem Kreis der Maßeinheit 1 Grad (Zeichen: 1°) im Gradmaß.

Bruchteile des Grad sind die Minute (Zeichen ') mit 1°=60', Bruchteile der Minute sind die Sekunden (Zeichen ") mit 1'=60"; die Dezimalschreibweise ist ebenfalls gebräuchlich.

Zusammenhang von Bogenmaß und Gradmaß

Mit dem Kreisumfang $2\pi r$ gilt die Proportion

zwischen Bogenmaß und Gradmaß.

Für kleine Winkel kann die Krümmung des Kreisbogens s vernachlässigt werden. Die Länge von s wird dann näherungsweise gleich der Länge der Gegenkathete a im rechtwinkligen Dreieck, siehe rechte Abbildung in der linken Spalte.

Wegen                                     $\frac{a}{b}\approx \frac{a}{r}=tan\phi$

gilt dann:                                    $tan\phi \approx \phi$,

wobei Werte für φ auf der rechten Seite im Bogenmaß vorliegt. In der Fernerkundung mit Lasern ist diese Beziehung nützlich, da die Laserstrahlen einen kleinen Öffnungswinkel besitzen und das Gesichtsfeld der Detektionsoptiken an diese kleinen Winkel angepasst wird, um störendes Fremdlicht so weit wie möglich fernzuhalten.