Supplement 3.1: Polar Coordinates
Cartesian coordinates
The positions of points, curves and areas in a plane are mostly given in Cartesian coordinates. It is an orthogonal coordinate system with a perpendicular orientation of the coordinate axes. The variables x and y are plotted in a right-handed system on the right-hand axis (the abscissa) and the vertical axis (the ordinate).
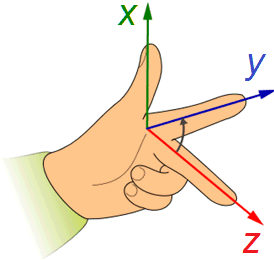
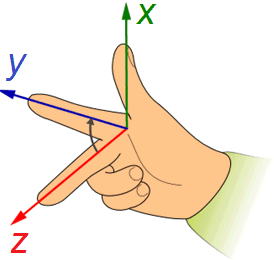
In a spatial orthogonal coordinate system, the z-axis is added, which is orientated perpendicular to the plane spanned by x and y.
Quite often, a given problem is easier explained and understood by considering the distance from the origin of the coordinate system and the angle from one of the coordinate axes. For example, the gravity of the earth acting on an object is always directed towards the geocentre, i.e., radially symmetric. With the geocentre as the origin of a coordinate system, it is much easier to derive the magnitude and direction of gravity acting on a satellite in space as a function of the distance and the angle from the polar axis than with Cartesian coordinates. Similar arguments apply to the propagation of light (including laser light) and to the observation of objects with the lens of a photocamera or a telescope: likewise, one finds a radial symmetry here.
Plane (2D) polar coordinates
A plane polar coordinate system uses the variables (r,φ) defined in the graph below, to describe the position of points, curves and areas.
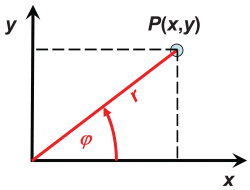
Conversion from Cartesian to polar coordinates:
Spherical (3D) polar coordinates
In addition to the x and y-axes, a 3D Cartesian coordinate system uses a z-axis oriented in a right-handed system as shown in the graph below. Correspondingly, the polar coordinates are
- the distance r from the origin,
- the angle φ from the x-axis (azimuth angle), and
- the angle ϑ from the z-axis (zenith angle)
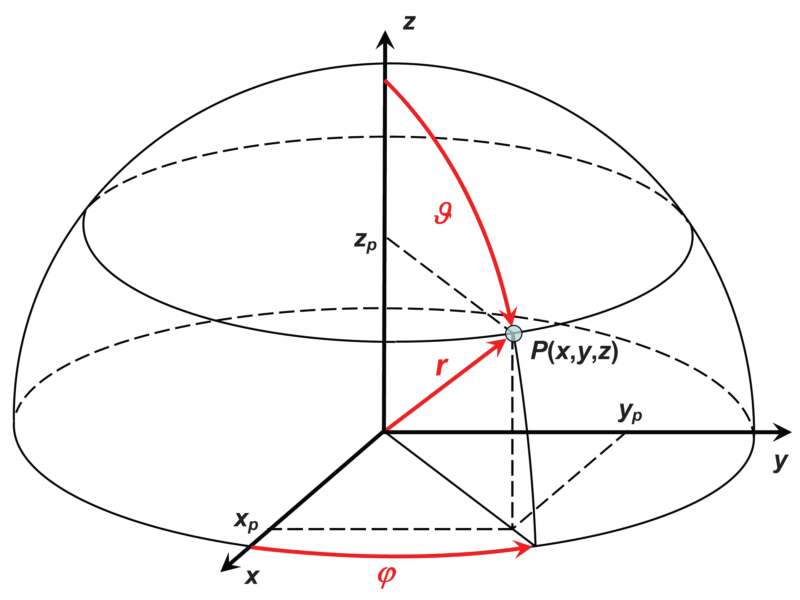
Conversion from Cartesian to polar coordinates, and vice versa:
A definition of plane and solid angles is found in Supplement 2. The geometry of light detecting instruments is analysed in Supplement 3.