Supplement 3.2: Plane and Solid Angles (1/2)

Plane angles

The angle φ of two intersecting straight lines, see left figure below, is given by the division of a circle around the point of intersection of the lines.

Left: The angle φ from the ratio of the arc length s and the radius r of a circle. Right: The same angle in a rectangular triangle, with the opposite leg a, the adjacent leg b, and the hypotenuse r.

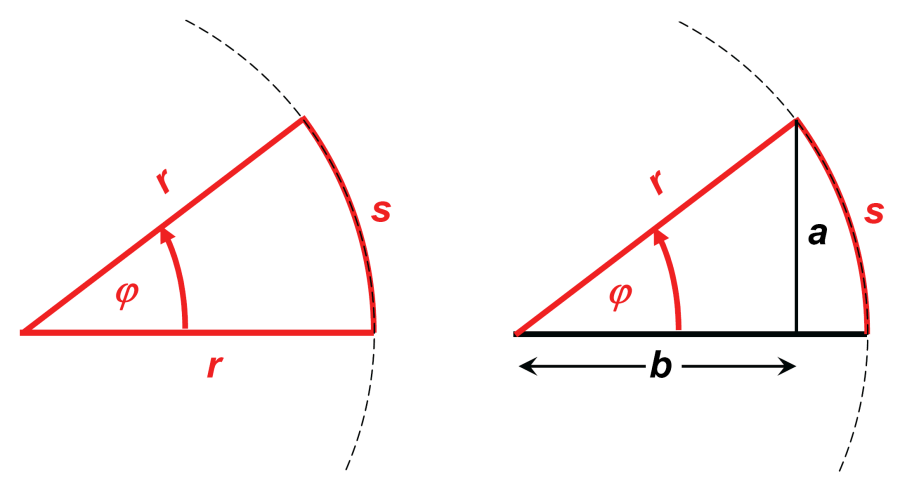
Radians

The ratio of arc length s and radius r defines the angle φ in radians:

Radians are without dimension and given with the symbol rad. Small angles are preferably given in milliradian, with the symbol mrad, with 1000 mrad=1 rad.

Degrees

The circumference is divided into 360 equal intervals. The orientational difference of two straight lines from the centre of the circle to two adjacent points on the circle corresponds to the unit 1 degree (symbol: 1°).

Fractions of a degree are expressed in minutes (symbol '), with 1°=60', fractions of a minute are expressed in seconds (symbol "), with 1'=60"; alternatively, parts of a degree can be given as decimals.

Relation of radians and degrees

Given the circumference $2\pi r$, the proportion between radians and degrees is

With small angles, the curvature of the arc length s can be neglected. The length of s and of the opposite leg a in the rectangular triangle are then approximately the same, see the right figure in the left column.

Since                                        $\frac{a}{b}\approx \frac{a}{r}=tan\phi$

it follows:                                    $tan\phi \approx \phi$,

where values of φ on the right side of the equation are given in radians. This relation is useful in laser remote sensing, since laser beams have a small divergence angle and the detector field of view is adapted to these small angles in order to keep disturbing daylight background as small as possible.