Supplément 4.3: Polarisation des ondes électromagnétiques, une introduction
La première approche
A la page 2 de la section sur les ondes électromagnétiques, nous avons développé des équations pour le champ électrique et le champ magnétique d'une onde plane monochromatique :
En raison du comportement périodique de la fonction sinus en , les équations montrent la périodicité avec la longueur d'onde λ et la période T. Au lieu de ces quantités, d'autres paramètres qui incluent le facteur sont utiles car les équations peuvent alors être écrites beaucoup plus brièvement. Ces paramètres sont les suivants :
- le nombre d'ondes
- la fréquence angulaire
Ce qui signifie que :
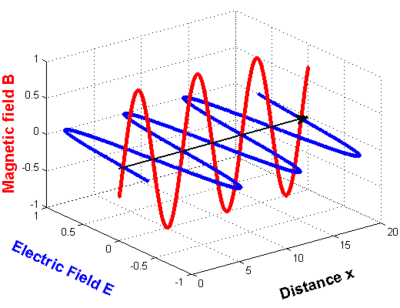
C'est ce à quoi ressemble l'onde dans un graphique :
Seules les ondes transversales - par exemple les ondes électromagnétiques - peuvent être polarisées. Les ondes longitudinales - par exemple les ondes sonores - ne sont pas polarisées.
Dans les graphiques ci-dessus, rien n'est dit sur la direction du champ électrique et du champ magnétique (si ce n'est qu'ils sont perpendiculaires l'un à l'autre et à la direction de propagation) : les coordonnées y et z manquent pour représenter la direction des vecteurs d'intensité du champ.
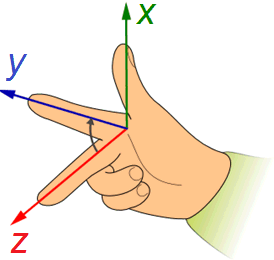
Nous examinons maintenant une onde qui se propage dans la direction x dans un système de coordonnées tridimensionnelles droites . Seul le champ électrique est examiné ; les résultats sont également valables pour le champ magnétique oscillant orthogonalement.
Le vecteur de champ est orthogonal à la direction de propagation x. Il est divisé en composantes le long des directions y et z:
et sont les amplitudes. La quantité indique le déphasage entre les deux composantes. Pour une onde monochromatique, est constante, les deux composantes de l'onde sont donc cohérentes.
Les principaux types de polarisation et leurs caractéristiques d'oscillation, étant un nombre entier :
| Condition | Type de polarisation |
|---|---|
| linéaire le long de l'axe y | |
| linéaire le long de l'axe z | |
| linéaire en diagonale dans les premier et troisième quadrants du plan y,z | |
| linéaire en diagonale dans les deuxième et quatrième quadrants du plan y,z | |
| circulaire droite : Les vecteurs de champ tournent à droite (face à la vague).
Animation des têtes de vecteurs tournantes, le champ E est représenté en bleu, le champ B en rouge. |
|
| circulaire gauche : Le vecteur de champ tourne à gauche (face à la vague) | |
| elliptique droite : Les vecteurs de champ tournent à droite (face à l'onde). Animation des têtes de vecteurs tournantes, le champ E est représenté en bleu, le champ B en rouge. |
|
| lumière naturelle non polarisée |
La lumière naturelle n'est pas monochromatique mais présente une large gamme spectrale, change de façon statistiquement permanente. Les composantes y et z ne sont pas cohérentes entre elles.
La lumière partiellement polarisée est composée de lumière polarisée et non polarisée. Elle est caractérisée par le degré de polarisation :