Ergänzung 3.6: Ein Experiment zur Lichtstreuung des Wassers
Lichtstreuung an Wasser, ein Beispiel für Rayleigh-Streuung
Der Absorptionskoeffizient des flüssigen Wassers ist bei allen sichtbaren Wellenlängen kleiner als 1/m. Im blauen Bereich ist Wasser besonders durchsichtig, dort ist der Absorptionskoeffizient etwa 0,02/m.
Der Streukoeffizient des Wassers ist im blauen Bereich noch einmal etwa einen Faktor 10 kleiner. Dies liegt an der verglichen mit der Lichtwellenlänge geringen Größe des Moleküls: sein Durchmesser ist etwa 2 Å oder 2·10-10 m (das Ångström, mit dem Einheitenzeichen Å, ist eine in der Atomphysik gebräuchliche Längeneinheit). Wassermoleküle sind daher ein Beispiel für Teilchen, die durch Rayleigh-Streuung charakterisiert sind.
Wir untersuchen hier, wie eine Wasserprobe das Licht eines Lasers streut.
Die experimentelle Anordnung
Eine wassergefüllte Küvette wird mit einem blaugrünen Laserstrahl beleuchtet. Die Wellenlänge ist 500 nm, die Strahlungsleistung ist 1 W (falls Sie den Versuch experimentell nachvollziehen möchten: der Laser wäre keineswegs augensicher, bitte äußerste Vorsicht!).
Unter 90° gegen die Richtung des Laserstrahls beobachten wir zunächst mit dem Auge das am Wasser entstehende Streulicht. Das beleuchtete und sichtbare Wasservolumen sei V = 1 cm3 groß.
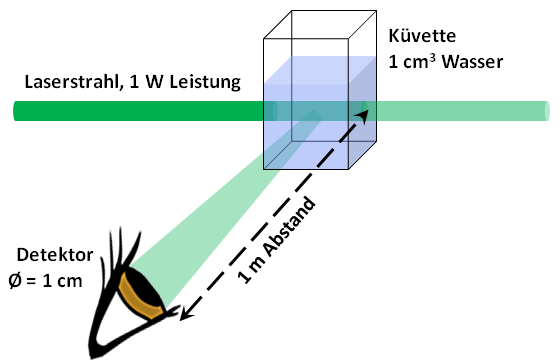
Quelle: Rainer Reuter, Universität Oldenburg.
Dann bringen wir für eine quantitative Messung in r = 1 m Abstand von der Küvette und ebenfalls unter 90° eine Fotodiode an. Der Durchmesser der fotoempfindlichen Fläche sei d = 1 cm. Bei 500 nm sei die Empfindlichkeit der Fotodiode, d.h. der von einer optischen Leistung (in Watt) erzeugte Fotostrom (in Ampere) der Diode, zu S = 0,5 A/W angenommen.
Streueigenschaften des Wassers
Sehr kleine Teilchen streuen das Licht symmetrisch in den vorderen und hinteren Halbraum, für die Rayleigh-Streuung kleiner Teilchen ist dies charakteristisch. Bezeichnet man den zur Richtung des Laserstrahls gemessenen Streuwinkel mit θ, so ist die Streufunktion für unpolarisiertes Licht durch die folgende Gleichung gegeben:
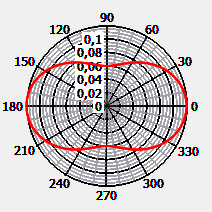
Erstellt mit MieSimulatorGUI, Version 1.3, letzter Zugriff: 30.03.2023.
Der Literaturwert der Streufunktion für den Streuwinkel 90° bei der Wellenlänge 500 nm ist (Zhang & Hu, 2021):
Die Molmasse des Wassers ist etwa 18 g, entsprechend ist das Molvolumen etwa 18 cm3. Die Teilchenzahl im Mol wird durch die Avogadro-Konstante 6·1023 gegeben. Die in 1 m3 enthaltene Zahl der Wassermoleküle wird dann:
Der differenzielle Wirkungsquerschnitt der Streuung bei 90° ergibt sich zu:
Die Helligkeit am Auge
Die Intensität des Streulichts folgt aus den Werten der Streufunktion β des Wassers und der Bestrahlungsstärke E des Lasers am beleuchteten Wasservolumen V entsprechend
mit E = 1 W/cm2 und V = 1 cm3. Die optische Leistung am Auge oder Detektor ergibt sich aus dieser Intensität multipliziert mit dem Raumwinkel Ω, unter dem vom streuenden Wasser aus gesehen das Auge bzw. der Detektor erscheint:
Das Einsetzen aller Werte liefert die optische Leistung P ≈ 10-10 W oder 0,1 Nanowatt. Kann das Auge dies noch sehen?
Um dies abzuschätzen ist es zweckmäßig, zum Photonenbild des Lichts überzugehen. Ein dunkel adaptiertes Auge kann etwa jedes 50ste auf die Netzhaut auffallende Photon als schwachen Lichtblitz wahrnehmen. Bei monochromatischem Licht gilt für den Zusammenhang zwischen optischer Leistung und der entsprechenden Photonenzahl:
mit NPhoton Zahl der Photonen pro Sekunde, und der Photonenenergie EPhoton = hc/λ, wobei h das Plancksche Wirkungsquantum und c die Lichtgeschwindigkeit bedeuten. Dies ergibt NPhoton ≈ 250· 106 oder 250 Millionen Photonen pro Sekunde.
Das Signal des Detektors
Der Fotostrom der Fotodiode ergibt sich aus der auffallenden optischen Leistung und aus seiner Empfindlichkeit, die oben zu S = 0,5 A/W angenommen worden ist. Es wird:
oder 50 Pikoampere. Elektrische Multimeter reichen bestenfalls bis in den Bereich Mikroampere, man benötigt daher ein sehr viel empfindlicheres Strommessgerät. Solche Geräte werden als Pikoamperemeter bezeichnet.
Der Streukoeffizient
Wird die Streufunktion über den ganzen Raum integriert, so resultiert der Streukoeffizient:
Einsetzen ergibt:
Über 1 m Strecke verliert der Laserstrahl durch Streuung demnach 2,3 Promille seiner Helligkeit. Die Abnahme der Helligkeit in der nur einen Zentimeter langen Küvette unseres Experiments ist praktisch zu vernachlässigen.
Der totale (über den ganzen Raum integrierte) Wirkungsquerschnitt der Streuung wird:
verglichen mit ihrer geometrischen Querschnittsfläche schatten die Moleküle somit nur einen sehr kleinen Teil der Helligkeit des Laserstahls ab.
