4. Absorption und Streuung

Etwas Mathematik

Wir beginnen mit einer Betrachtung auf kleinsten - infinitesimalen - Skalen in einer absorbierenden Substanz, die von links beleuchtet wird. An der Stelle $x$ hat das Licht die Intensität $I$ . Eine Infinitesimale Strecke $d x$ entfernt, also an der Stelle $x + d x$ , hat die Intensität um einen infinitesimalen Wert $d I$ abgenommen, sie ist daher $I - d I$ .

Licht breitet sich in einem absorbierenden Medium von links nach rechts aus. An der Stelle x ist die Intensität gleich I, an der Stelle x+dx ist sie auf I-dI gesunken.

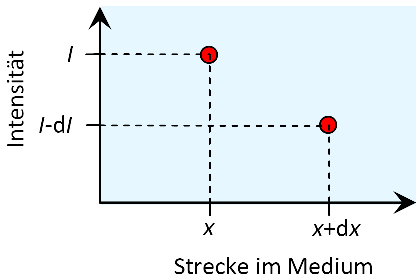
Die Abnahme $- d I$ kann man als proportional zu $I$ und zu $d x$ annehmen:

- d I ~ I d x

Darüber hinaus wird sie auch vom Absorptionsverhalten der Substanz abhängen. Diese stoffspezifische Eigenschaft soll durch den Absorptionskoeffizienten a charakterisiert werden, mit dem die Proportionalität zu einer Gleichung wird:

- d I = a I d x

Umformen führt zu der Differenzialgleichung

\frac{d I}{d x} = - a I

die nun gelöst (oder: integriert) werden muss. Fasst man die Gleichung in Worte, lässt sich die Lösung (das Integral) leicht finden:

"Gesucht ist die Intensität $I$ , ..."
linke Seite: "... deren Ableitung nach $x$ ..."
rechte Seite: "... wiederum $I$ mit dem zusätzlichen Faktor $- a$ ergibt."

Die Funktion, die dies tut, ist die Exponentialfunktion: sie bleibt beim Ableiten und Integrieren erhalten. Ein Ansatz zur Lösung ist also

I = e^{- a x}

was abgeleitet nach $x$ wieder zur Differenzialgleichung führt:

\frac{d I}{d x} = - a e^{- a x} = - a I

Die Exponentialfunktion ist also der richtige Ansatz zur Lösung.

An der Stelle $x = 0$ soll die Intensität gleich $I_{o}$ sein (das sei die Anfangsintensität, der bisherige Ansatz ergibt bei $x = 0$ den Wert 1), was im Ansatz zur Lösung auf der rechten Seite ergänzt wird und zur endgültigen Lösung führt:

I (x) = I_{o} e^{- a x}

Exponentiell oder linear? ↓

In der linken Spalte hatten wir die infinitesimale Abnahme $- d I$ als proportional zur infinitesimalen Strecke $d x$ angenommen. Proportionales Verhalten lässt vermuten, dass die Intensität linear über der Strecke $x$ abnimmt. Nun haben wir gefunden, dass die Intensität aber exponentiell abnimmt. Wie passt das zusammen?

Antwort: (aber überlegen Sie doch erst mal selbst!)
Die Exponentialfunktion kann über eine infinitesimale Strecke $d x$ durch eine Tangente angenähert werden, deren Steigung sich aus $d I / d x = - a e^{- a x}$ und dem Einsetzen des jeweiligen $x$ -Werts ergibt. Dies entspricht dem linearen Ansatz auf unendlich kleinen Skalen. Über endlich große Strecken betrachtet, d.h. nach der Integration der Differenzialgleichung, ergibt sich dann die Exponentialkurve.

Gleichungen ↓

Das Lambertsche Gesetz: die Intensität des Lichts nimmt über die Strecke x exponentiell ab. Die folgenden Fotos zeigen dies am Beispiel der Absorption von Laserlicht durch grüne Pflanzenpigmente.

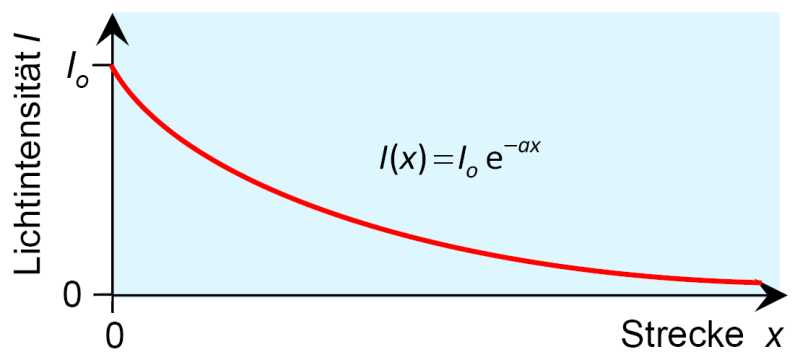
Dies ist das Lambertsche Gesetz: die Intensität des Lichts nimmt auf dem Weg durch ein absorbierendes Medium exponentiell ab, wobei die Höhe der Abnahme vom Absorptionskoeffizienten $a$ abhängt.

405 nm 532 nm 650 nm Chlorophyll-Absorption

Chlorophyll a wurde mit Alkohol aus Pflanzenblättern herausgelöst. Eine Glasküvette mit der grün gefärbten Lösung wird von links mit Laserstrahlen durchleuchtet. Chlorophyll absorbiert blaues Licht, die Helligkeit des blauen Strahls (Wellenlänge 405 nm) nimmt daher von links nach rechts deutlich ab. Das rote Leuchten entsteht durch die rote Fluoreszenz des Chlorophylls, wenn es mit blauem Licht beleuchtet wird. Der grüne Laserstrahl (532 nm) zeigt keine merkliche Helligkeitsabnahme, der rote Laserstrahl (650 nm) nur eine geringe. Die Helligkeit nimmt unterschiedlich in der Küvette ab, in Abhängigkeit von der Chlorophyll-Absorption bei der Wellenlänge des benutzten Lasers.
Quelle des Chlorophyll a-Absorptionsspektrums: PhotochemCAD. Das Spektrum zeigt den molaren dekadischen Absorptionskoeffizienten, was aber erst in der Ergänzung 4.1 behandelt wird.

Der Absorptionskoeffizient hat die Dimension einer inversen Länge. Er wird je nach seinem Wert zweckmäßig in unterschiedlichen Einheiten angegeben:

für die klare Atmosphäre meist in 1/km,
für Gewässer in 1/m,
für stark absorbierende Stoffe (zum Beispiel Ölverschmutzungen in der Umwelt) in 1/μm.

Spektren der Erde

4. Absorption und Streuung

Etwas Mathematik