Supplément 2.6 : Différentielles et dérivées (4/4)
La vitesse d'écoulement, un exemple de vecteur
Le formalisme donné jusqu'à présent est valable non seulement pour les quantités scalaires telles que la température, mais aussi pour les vecteurs, par exemple le vecteur vitesse. En remplaçant dans l'équation
par , on obtient :
Les notations « forme lagrangienne et eulérienne » ainsi que « terme convectif » sont utilisées de la même manière. Il convient toutefois de prêter une attention particulière aux parenthèses. Qu'est-ce que cela signifie ?
Le terme dans l'exemple de la température est le produit scalaire des vecteurs et . L'ordre de multiplication n'a pas d'importance dans ce cas : il est également correct de calculer d'abord et de multiplier ensuite le résultat scalaire par .
Cependant, le terme n'est pas défini, c'est pourquoi l'ordre de multiplication a son importance ici. Ceci est clarifié par les parenthèses dans le terme . Le produit scalaire entre parenthèses devient
et le résultat - un scalaire - est multiplié par ,
ses composantes cartésiennes :
Par conséquent, la dérivée totale de la vitesse dans les composantes devient :
Il s'agit des relations cinématiques fondamentales utilisées pour la description physique des courants : elles spécifient l'accélération de milieux déformables tels que l'air et l'eau.
En ajoutant d'autres termes d'accélération qui résultent des forces en tant que cause et effet de l'accélération, on obtient l'équation de la quantité de mouvement hydrodynamique. Si le frottement fait partie des forces, le résultat sera l'équation de Navier Stokes de l'hydrodynamique.
Le graphique suivant montre les trajectoires des dériveurs de surface, avec une barre de couleur dans cet exemple, qui indique la vitesse de dérive en m/s. On constate que la vitesse de dérive est très variable et peut en outre prendre des valeurs élevées en haute mer. Il s'agit d'un exemple de représentation lagrangienne des courants.
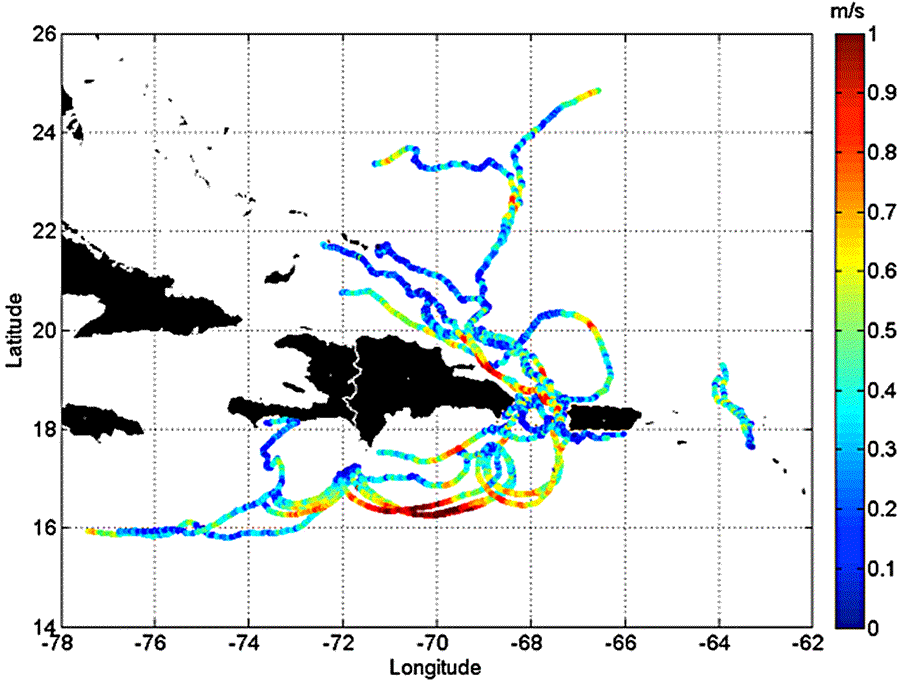
Source: Caribbean Coastal Ocean Observation System (Caribbean IOOS).
Le graphique suivant montre une série temporelle de courants océaniques sur deux jours dans la mer des Wadden de Basse-Saxe, près de l'île de Spiekeroog. Le diagramme montre la vitesse du courant, qui est caractérisée par le cycle d'une demi-journée des marées, et la direction du courant, qui est dominée par la direction nord-sud à travers l'entrée de la marée de Spiekeroog. Il s'agit d'un exemple de représentation eulérienne de la vitesse du courant.
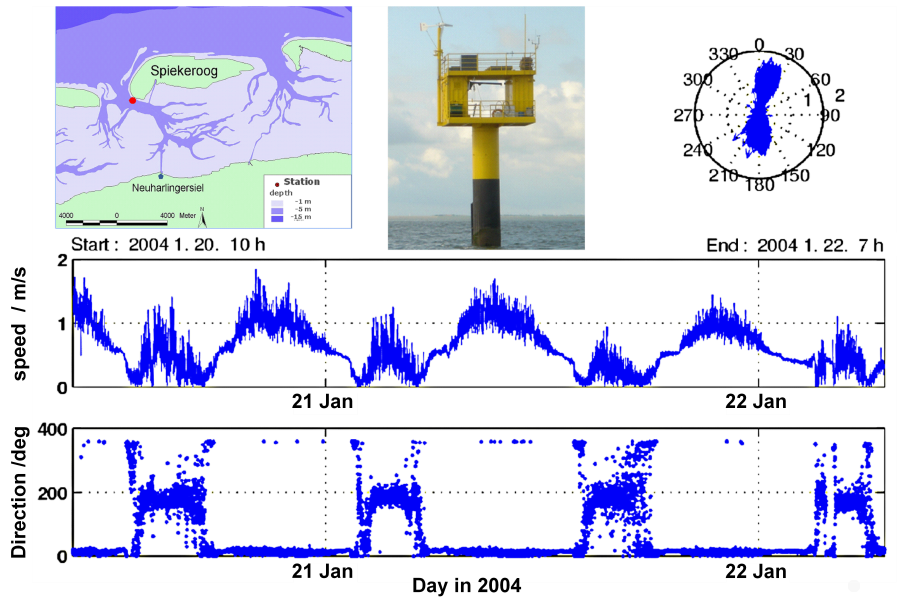
L'altimétrie radar par satellite permet de déterminer les courants océaniques globaux à partir de la topographie mesurée de la surface de l'océan. Pour cet aspect, vous pouvez trouver une vidéo réalisée il y a plusieurs années par le Scientific Visualization Studio de la NASA avec des liens supplémentaires comme exemple d'une représentation lagrangienne des courants océaniques.
