2. Temperatuurstraling

De kleur: de verplaatsingswet van Wien

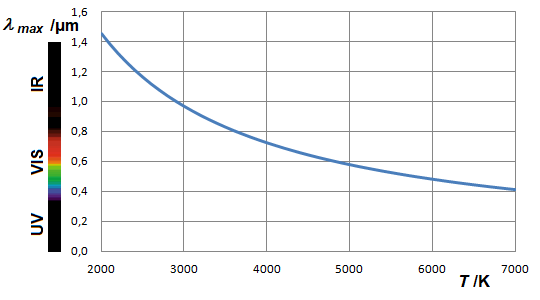
Het gebied onder de spectra van zwarte lichamen is voor ons even interessant als de golflengten waarvan de Planck-spectra hun hoogste waarde bereiken. Dit maximum lijkt alleen af te hangen van de temperatuur, met een tendens naar kleinere golflengten bij een toenemende temperatuur. Als we de Planck-spectra als een frequentierepresentatie beschouwen, zien we een tendens naar hogere frequenties van de maxima bij toenemende temperatuur. Op welke functionele afhankelijkheid is dit gebaseerd?

We vertrekken van de frequentierepresentatie van de spectrale energiedichtheid zoals we deden bij de bespreking van de wet van Stefan-Boltzmann.

u f = dU df = 8πh c 3 f 3 exp{ hf / kT }−1

Het zoeken naar het maximum van de stralingswet is een extremumprobleem van wiskundige analyse: het afleiden en op nul stellen van de afgeleide. Dit is enigszins moeilijk omdat het een transcendentale vergelijking is: fmax wordt gevonden in de eerste macht en tegelijkertijd als de exponent van de e-functie. De gedetailleerde berekening staat in Supplement 2.4.

Het resultaat is:

f max T =5.879⋅ 10 10 1/ (s·K)

De frequentie van het stralingsmaximum van een zwart lichaam neemt evenredig toe met de temperatuur.

De positie van het maximum als functie van de golflengte volgt uit een analoge berekening, zie Supplement 2.4. Het resultaat is:

λ max T=2.90⋅ 10 −3 m·K

In dit geval vinden we een omgekeerde evenredigheid: de maxima van de Planck-grafiek als functie van de golflengte volgen een hyperbool.

Dit wordt de verplaatsingswet van Wiengenoemd.

De maxima van de stralingswet van Planck veranderen hun spectrale locatie op een opmerkelijk duidelijke manier: de golflengte van het maximum vermenigvuldigd met de absolute temperatuur is een constante. Of: de verhouding tussen de frequentie van het maximum en de absolute temperatuur is een constante.

 

Maximaal bij 2000 - 7000 K Maximaal bij 100 - 2000 K
Maximaal bij 2000 - 7000 K
Golflengte in µm van het stralingsmaximum voor zwarte lichamen. Links: Bij temperaturen tussen 2000 en 7000 K. Het stralende zonneoppervlak heeft een temperatuur van ongeveer 5800 K. Rechts: Bij temperaturen tussen 100 en 2000 K. 300 K komt ongeveer overeen met kamertemperatuur.
Bron: Rainer Reuter, Universiteit van Oldenburg, Duitsland.

Als we één waardepaar kennen, kan de golflengte van de frequentie van het maximum voor elke andere temperatuur worden berekend met behulp van de regel van drie. Het is dus niet nodig om de waarde rechts van de verplaatsingswet van Wien te onthouden. Het is voldoende om te weten dat:

λ max ⋅T=const.
Opdracht: Maxima van de Planck-grafiek van verschillende radiatoren ↓