2. Temperatuurstraling

De rol van temperatuur: de wet van Stefan-Boltzmann

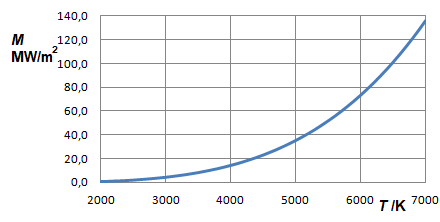
We zijn geïnteresseerd in het gebied onder de Planck-spectra van zwarte lichamen, die in de vorige paragraaf zijn besproken. Het is duidelijk dat deze gebieden groter worden naarmate de temperatuur van de straler toeneemt. De manier waarop dit gebeurt zal worden gevonden door de oppervlakte onder de grafieken te bepalen.

De berekening van het gebied resulteert uit de integratie van de Planck-grafieken. Uitgaande van de frequentieafbeelding van de spectrale energiedichtheid

u_{f} = \frac{d U}{d f} = \frac{8 π h}{c^{3}} \frac{f^{3}}{exp {h f / k T} - 1}

Door integratie verkrijgt men de energiedichtheid van alle mogelijke frequenties

U = \int_{f = 0}^{\infty} u_{f} d f = \frac{8 π h}{c^{3}} \int_{f = 0}^{\infty} \frac{f^{3}}{exp {h f / k T} - 1} d f

Het berekenen van de integraal kan enigszins lastig zijn. De procedure wordt getoond in Supplement 2.3. Het resultaat is:

U = \frac{8 π^{5} k^{4}}{15 c^{3} h^{3}} T^{4}

De specifieke emissie $M$ gegeven W/m² van een zwart lichaam, bijvoorbeeld het stralingsvermogen dat uit de opening van een holtestraler komt, is in de meeste gevallen betekenisvoller voor praktische toepassingen dan de energiedichtheid in (Ws)/m³ resp. J/m³ aan de binnenkant van de holte. De relatie is:

M = \frac{c}{4} U

Het resultaat is de wet van Stefan-Boltzmann:

M = \frac{2 π^{5} k^{4}}{15 c^{2} h^{3}} T^{4} = σ T^{4}

Vergelijkingen ↓

Met $h = 6.6 \cdot 10^{- 34} Js$ , $k = 1.38 \cdot 10^{- 23} J/K$ en $c = 3 \cdot 10^{8} m/s$ wordt de constante van Stefan-Boltzmann verkregen:

σ = 5.670 \cdot 10^{- 8} \frac{W}{m^{2} K^{4}}

De straling neemt dan ook onevenredig toe met de vierde macht van de temperatuur. Een verdubbeling van de temperatuur van bijvoorbeeld 300 K (kamertemperatuur) tot 600 K (327°C, smeltpunt van lood) resulteert in een 16-voudige toename van de straling!

Totale straling voor 2000 - 7000 K Totale straling voor 0 - 2200 K

Totale straling

M

van zwarte lichamen. Links: In MW/m² bij temperaturen tussen 2000 en 7000 K. Het stralende zonneoppervlak heeft een temperatuur van ongeveer 5800 K. Rechts: In kW/m² bij temperaturen tussen 0 en 2200 K. 300 K komt ongeveer overeen met kamertemperatuur.
Bron: Rainer Reuter, Universiteit van Oldenburg, Duitsland.

Inzicht in Spectra van de Aarde

2. Temperatuurstraling

De rol van temperatuur: de wet van Stefan-Boltzmann