2. Thermal Radiation

Light as a particle: Planck's radiation law     (1/2)

Max Planck worked theoretically on radiation in isolated cavities as mentioned on the previous pages. Those are in a thermal equilibrium and have ideally absorbing walls. Lighting inside with a lamp through a small opening, all the light is absorbed on the inner walls so that no light comes out through the opening. The inner space is hence a black body. Due to this feature it is also called a black body emitter or cavity radiator.

From 1890 on, the outcoming light of the cavity was experimentally examined in the Lichttechnisches Labor of the Physikalisch-Technische Reichsanstalt in Berlin for what Planck could take advantage of highly precise experimental data.

Radiation as a function of the frequency

Planck was particularly interested in the energy density U of the cavity radiation, which has already been mentioned in supplement 1.4; it describes the radiative energy in a volume and is given in units of J/m³ or (Ws)/m³. Here the spectral dependence of the energy density is of interest and we write it as a function of the frequency:

dU df = u f

The equation for the spectral energy density found by Planck in 1900 and correlating well with the measured data is:

u f = dU df = 8π f 2 c 3    hf exp{ hf / kT }−1 ,

with the Planck constant h, the speed of light c and the Boltzmann constant k=1.38⋅ 10 −23  J/K . In order to find this equation he had to assume that light, i.e., electromagnetic waves are made up of quanta, named photons later-on. The energy of these quanta should be given by E=hf. Planck's calculus is outlined in supplement 2.2.

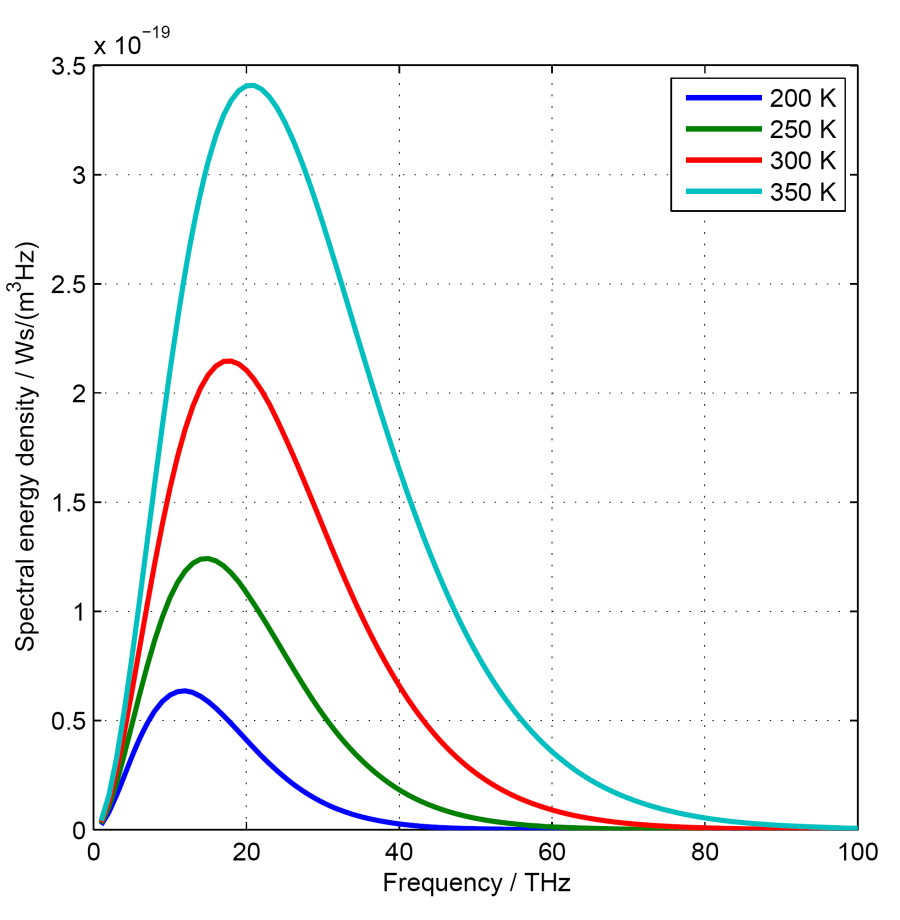
Examples of spectral energy density curves for black bodies are shown in the image on the right. They are calculated for temperatures between 200 and 7000 K (corresponding to about -70° and +6730° Celsius).

Planck's publications ↓
It is remarkable that the energy density depends on T only: The temperature is the only variable.

Other quantities, especially the material properties of the emitter do not play a role. It can be a solid object, a liquid or a gas.

Equations ↓

Beyond any relevance as well is the amount of heat stored in a black body. This becomes evident by the degree of absorption α=1: It is just the opaque surface layer of the body which emits because the internal matter entirely absorbs any radiation.

In consequence, at the place of the often heard term heat radiation, the term thermal radiation is more appropriate.

In order to better recognise the temperatures in the graphics:

  • room temperature is about 300 K
  • temperature of red heat equals about 1500 K
  • the sun emits at surface temperatures of about 6000 K

200-400 K 400-1000 K 1000-2500 K 2500-4000 K 4000-7000 K
200-350 K
Emission graphs of black bodies as a function of frequency at different temperatures in Kelvin.

A third remarkable property of black body radiation: the emission graphs of bodies having different temperatures do not intersect. Instead, the emission of a hot emitter is higher at all frequencies or wavelengths than the emission of a colder emitter.