Supplement 2.2: Planck's Radiation Law    (1/2)

Max Planck supposed the concept of a cavity: Its radiation is in thermal equilibrium with the surface of the internal space. The surface's atoms absorb all incoming radiation. Meanwhile they send out electromagnetic waves obeying Kirchhoff's radiation law with the highest degree of emission $\epsilon =1$ possible for black bodies.

A second conceptual reflection concerns the waves' energy that is emitted by the atoms of the surface. These waves are interlinked to the oscillating atoms, the so-called oscillators. As per classical physics, such energy values are distributed continuously: The energy of oscillation in a classical oscillating system can take continuously distributed values. Planck supposed that these energies are quantized, though. Therefore, they could take only discrete values. This contradicted classical physics but led to the right conclusion and therefore it represents the basis of a new development, the quantum theory.

Waves in a cavity

We observe a small range of the spectrum at a frequency $f$ and the present energy density $\text{d}U=u_f\text{d}f$ of the waves in an infinitesimal frequency interval $\text{d}f$. It is seemingly expressible through the midspectral energy density of a single wave, multiplied by the existing waves in the interval $\text{d}f$.

The number of these waves can be estimated. In accordance with the Maxwell theory of electromagnetic waves, the electric field strength shall be zero at the surface. This is where only stationary waves with nodes of oscillation can appear, if their wavelength in a cavity of the inner extent $L$ qualifies as:

Further holds: $n=\mathrm{0<mo>,</mo>}\mathrm{1<mo>,</mo>}\mathrm{2<mo>,</mo>}\mathrm{3<mo>,</mo>}\mathrm{...}$ Only integer multiples of the bisected wavelength fit in with the distance $L$, if a node is supposed to appear at the edges. The possible wavelengths hence are not continuous but discretely distributed; they form the intrinsic osillations, known as modes, of the cavity.

The wave numbers resp. frequencies therefore correspond to:

Reforming the last relation and differentiating it, for the demanded number of oscillation modes in the frequency interval follows:

Now there is the three-dimensionality of the cavity to be considered, such as the waves characteristics to oscillate in three dimensions x, y and z. Correspondingly there are discrete number values n_x, n_y and n_z will result for these coordinate directions. How many waves $\text{d}N$ are present in the void in total?

In order to find that, we examine the waves in a three-dimensional space with the coordinates n_x, n_y and n_z. The corresponding waves to the frequency interval $\text{d}f$ lay in a sperical shell of that space with the radius

and the thickness $\text{d}n$. Their volume results from multiplication of the sphere's surface with the shell's thickness $4\pi n^2\text{d}n$.

Exclusively positive values for n_x, n_y and n_z are legitimate (the wavelengths in the conditions for stationary waves are positive). Only in one of the eight octants of the coordinate system, all values are positive. Thus, this is the only one permitted.

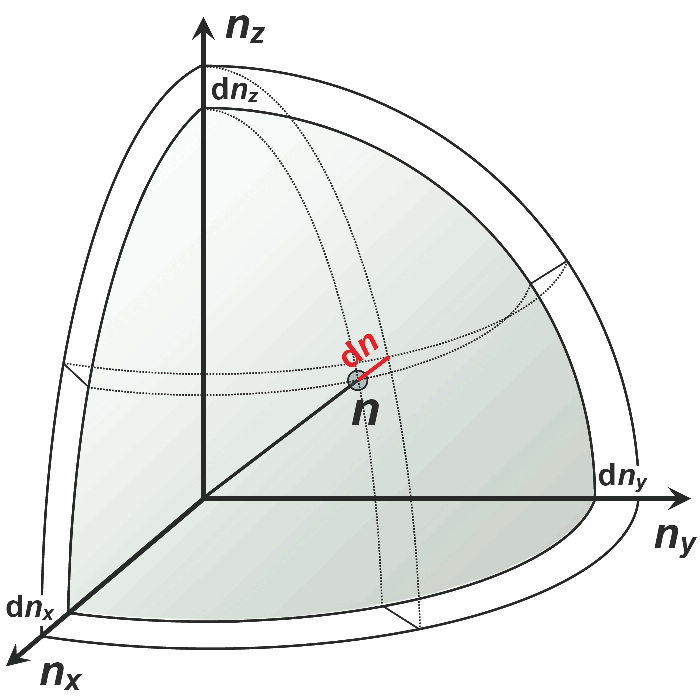
Three-dimensional space of possible oscillator modes of stationary waves in a cavity. Only the octant with exclusively positive values is depicted.

Every wave can appear with two orthogonal polarisations what is to be taken into account through the factor 2. This delivers the number of oscillation states by applying the arithmetic expressions for $n$ and $\text{d}n$:

While doing so, without limitation of the generality, it's supposed that the cavity has the same expansion $L$ in all three dimensions. With the volume $V=L^3$ the number of modes of the void in the frequency interval $\text{d}f$ is obtained: