6. Erreurs et coûts dans la classification

Essayons de faire la distinction entre deux classes de distribution normale, comme montré sur la figure ci-dessous.

Sur cette image, les pixels ayant une valeur se situant à gauche de la surface de décision seront assignés à la classe A, et ceux à droite à la classe B. Mais on peut voir que cela amènera certaines erreurs, puisque quelques pixels de la classe A se situeront à l'extrémité droite de la distribution, et occuperons donc l'espace G, tout comme des pixels de la classe B occuperont la zone H. La classification souffrira donc toujours d'erreurs. Les zones G et H représentent les probabilités de mauvaise classification de pixels dans les classe A et B respectivement.

L'importance des erreurs peut être réduite en utilisant des données pour lesquelles les classes se superposent moins. Quoi qu'il en soit, une fois les données sélectionnées, les erreurs ne peuvent plus être réduites, mais changer la surface de décision peut changer la distribution des erreurs. Par exemple, on peut changer la surface de décision pour qu'il y aie plus d'erreurs dans une classe que dans l'autre.

Généralement, on fixe la surface de décision pour avoir la même probabilité d'erreurs dans les deux classes, donc pour que l'aire de G = l'aire de H, c'est-à-dire la surface de décision de gauche sur la figure.

Il est possible que les coûts associés aux erreurs dans la classe A soient plus grands que les coûts associée à une mauvaise classification dans la classe B. Dans ce cas, il vaut mieux bouger la surface de décision pour que :

(Probabilités de mauvaise classification de A) · (coût de mauvaise classification de A) = (Probabilités de mauvaise classification de B) · (coût de mauvaise classification de B)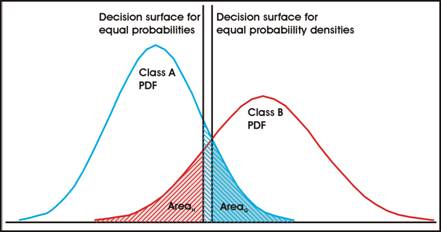
Zoom Sign
Deux classes dans une dimension, leurs distributions normales et deux surfaces de décision possibles, qui pourraient être utilisées pour assigner des objets aux deux classes.

Si le coût de mauvaise classification de A est plus grand que celui de B, la surfaceG, représentant la probabilité de mauvaise classification de A, doit être réduite. Cela implique bien sur que la surfaceH sera plus grande.

Donc : AireG · CoûtA = AireH · CoûtB

On sait, via les fonctions de densité de probabilité, que :

Air e G =Pr{(x> x d )|N( x ¯ A , σ A 2 )} et Air e H =Pr=( x ¯ < x d )|N( x B , σ B 2 )}

Donc, nous devons ajuster la surface de décision en changeant xd jusqu'à ce que la condition spécifiée dans la première équation soit remplie.