Het Corioliseffect
In welk kader zit je?
Wees niet verbaasd als je te horen krijgt dat beweging altijd relatief is aan een referentiekader. Per slot van rekening, als je comfortabel een boek zit te lezen op een trein die met 100 km/u door een station rijdt, is je boek nog steeds relatief ten opzichte van jou (d.w.z. in een referentiekader dat met de trein mee beweegt). Maar zowel jij als je boek verplaatsen zich met 100 km/h ten opzichte van een waarnemer die op het perron van het station staat.
Beweging is niet het enige dat van het referentiekader afhangt, maar ook de krachten die men ervaart. Dus wanneer de trein met een constante snelheid op een rechte spoorlijn rijdt, dan voel je geen kracht, maar wanneer hij accelereert, voel je een kracht die je achteruit trekt en wanneer hij remt, voel je een duw naar voren. En wanneer de spoorweg een bocht maakt, voel je een duidelijke ruk naar de buitenkant van de bocht - de welbekende centrifugale kracht die opgevangen moet worden door een goed gebouwd, stevig spoor - anders zou de trein ontsporen (!) en een fles water op je tafel zou kunnen omvallen als de bocht te snel wordt genomen.
De krachten die je voelt wanneer de trein accelereert, remt en een bocht maakt, worden fictieve krachten genoemd - ze worden enkel gevoeld door de passagiers op de trein, of met andere woorden ze bestaan enkel in een referentiekader dat met de trein meebeweegt. Maar je moet hen uitleggen wat er gebeurt vanuit het oogpunt van de passagier - anders zou er geen verklaring zijn voor het omvallen van de fles, bijvoorbeeld. Telkens als je beweging wilt bestuderen, moet je deze uitdrukken ten opzichte van een referentiekader.
De draaiende aarde als referentiekader
Wanneer meteorologen en oceanografen de atmosfeer en oceanen op onze planeet bestuderen, moeten ze ook een referentiekader kiezen. Het is niet te verbazen dat de meest gebruikelijke een is die met de Aarde zelf draait en waarin, bijgevolg, de aarde stilstaat. Dit stemt overeen met het gezichtspunt van iemand die op de aarde staat (in tegenstelling tot een buitenaards wezen dat vanuit de ruimte naar de aarde kijkt!). Dus, dit is de meest natuurlijke benadering voor iemand die de grond als stilstaand beschouwt.
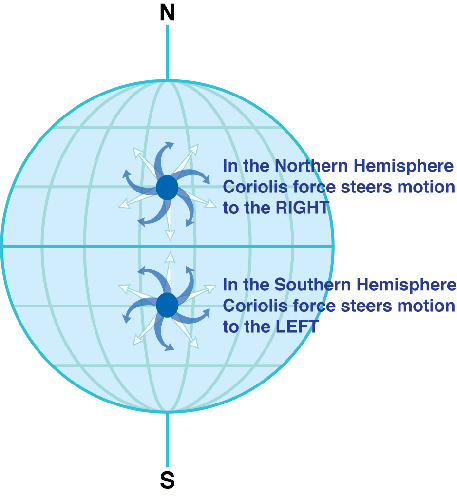
In het zuiden draait de Corioliskracht de beweging naar links.
Het merendeel van de bewegingen waarmee we dagelijks te maken hebben, van het slingeren van de slinger van een klok tot de baan van een bal op een snookertafel tot de vlucht van een vliegtuig, kan vlot in dit referentiekader uitgedrukt worden met een zeer goede benadering zonder de noodzaak van enige fictieve krachten. Maar wanneer we naar bewegingen op grote schaal kijken (van de grootteorde van honderden of duizenden km, kenmerkend voor stromen en winden), dan gebeuren er een paar vreemde dingen, die enkel verklaard kunnen worden door een fictieve kracht veroorzaakt door de draaiing van onze planeet: de Corioliskracht.

Inzicht in Coriolis op een draaimolen
Om het Corioliseffect met een eenvoudig voorbeeld te begrijpen, beeld je in dat je op een draaiende draaimolen zit (laten we zeggen met een snelheid van één volledig omwenteling om de zoveel seconden) en je gooit een bal horizontaal. Vanuit het oogpunt van een externe waarnemer (dat is iemand die vanaf buiten naar de draaimolen kijkt) beweegt de bal in een rechte lijn, maar vanuit jouw oogpunt (dat is een referentiekader dat meedraait met de draaimolen) zal de baan van de bal gebogen zijn. Bijvoorbeeld als de draaimolen tegen de wijzers van de klok draait, zal de bal zoals door jou gezien, naar rechts afwijken zoals bovenstaand filmpje laat zien.
Dit afbuigen van de baan staat bekend als het Corioliseffect.
In je (draaiend) referentiekader moet je een extra kracht hebben om te verklaren wat er gebeurt. Die fictieve kracht staat bekend als de Corioliskracht.
Corioliskracht bij atmosferische en oceaanbeweging
De tijds-, ruimte- en snelheidsschalen van de beweging zijn belangrijk bij het bepalen of het Corioliseffect belangrijk of te verwaarlozen is. Eerst en vooral, de Corioliskracht ontstaat enkel voor een voorwerp in beweging ten opzichte van het referentiekader. De aarde draait zoals de draaimolen in het bovenstaande voorbeeld, maar met een veel lagere snelheid. Dit betekent dat het Corioliseffect veroorzaakt door de draaiing van de aarde enkel belangrijk is voor bewegingen op een schaal langer dan een paar tientallen kilometer, zoals die van stromen of atmosferische straalstromen.
Het resulterend effect is dat op het noordelijk halfrond deze stromen naar rechts afbuigen, terwijl op het zuidelijk halfrond deze naar links afbuigen. Op de evenaar is het Corioliseffect in de horizontale richting nul. Er is een kleine duw of ruk op een bewegend lichaam (afhankelijk van in welke richting het lichaam zich verplaatst), maar het gaat in de verticale richting en is veel kleiner dan de zwaartekracht van de Aarde.
