The Coriolis Effect

Which frame are you in?

You should not be surprised to learn that motion is always relative to a reference frame. After all, if you are comfortably reading a book, sitting on a train travelling at 100 km/h across a station, your book is still relative to you (i.e. in a reference frame moving with the train); but both you and your book are moving at 100 km/h with respect to an observer standing on the station platform.

It is not just motion which depends on the reference frame, but also the forces that one experiences; so, when the train goes at constant speed on a straight track you feel no force, but when it accelerates you feel a force pulling you backwards, and when it brakes you feel a push forward. And when the track turns, you feel a distinctive pull towards the outside of the curve – the well-known centrifugal force, which must be borne up by a well-built robust railtrack – otherwise the train would derail (!) and a bottle of water on your table may well topple if the curve is taken too fast.

The forces that are experienced when the train accelerates, decelerates and turns are called fictitious forces – they are only felt by the passengers on the train, or in other words they only exist in a reference frame moving with the train. But you need them to explain what happens from the point of view of the passenger – otherwise there would be no explanation of the toppling bottle, for instance. Every time you want to study motion, you need to express it with respect to a reference frame.

The rotating Earth as a reference frame

When meteorologists and oceanographers study atmosphere and oceans on our planet, they also need to elect a frame of reference. Not surprisingly, the most common is one that is rotating with the Earth itself and in which, therefore, the Earth is stationary. This corresponds to the point of view of someone standing on the Earth’s (as opposed to an alien watching earth from space!) So it is the most natural approach for someone who considers the ground still.

 

The vast majority of motions that we see in our every day’s experience, from the swing of a clock’s pendulum to the trajectory of a ball on the snooker table to the flight of an airplane, can readily be expressed in this reference frame with very good approximation without the need of any fictitious forces. But when we look at large-scale motions (of the order of hundred or thousands of km, typical of currents and winds), then some strange things happen, which can only be explained by the action of a fictitious force due to the rotation of our planet: the Coriolis force.

Understanding Coriolis on a carousel

To understand the Coriolis effect with a simple example, imagine that you are sitting on a rotating carousel (say, at a rate of one full revolution every few seconds) and you throw a ball horizontally. From the point of view of an external observer (i.e someone who is watching the carousel from outside) the ball moves in a straight line, but from your point of view (i.e. on a reference frame rotating with the carousel) the trajectory of the ball will be curved. For instance, if the carousel spins counterclockwise, the ball as seen by you, will deviate to the right as shown in the movie above.

This curving of the trajectory is known as the Coriolis Effect.

In your (rotating) reference frame, you need an extra force to explain what is happening. That fictitious force is know as the Coriolis Force.

Coriolis force in atmospheric and oceanic motion

The time, space and velocity scales of the motion are important in determining whether the Coriolis effect is important or negligible. First and foremost, the Coriolis force arises only for an object in motion with respect to the frame of reference. The Earth is rotating like the carousel in the example above, only at a much slower rate. This means that the Coriolis effect due to Earth’s rotation is only important for motions of a scale longer than a few tens of kilometres, such as those of currents or atmospheric jets.

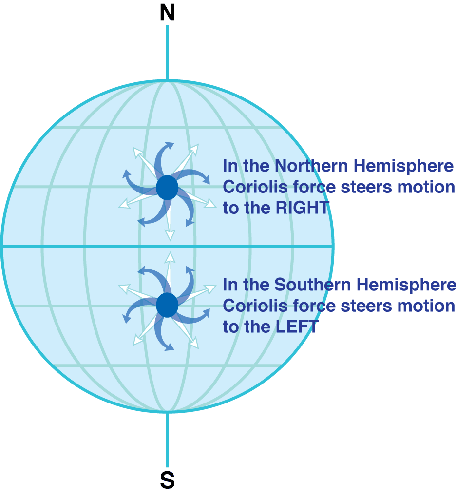
The resulting effect is that in the Northern Hemisphere these flows veer to the right, while in the Southern Hemisphere they veer to the left. At the equator the Coriolis effect in the horizontal direction is zero – there is a tiny push or pull on a moving body (depending on which direction the body is travelling) but it goes in the vertical direction and is much smaller than Earth’s gravity pull.