Exercice c02-02-4

Scenario

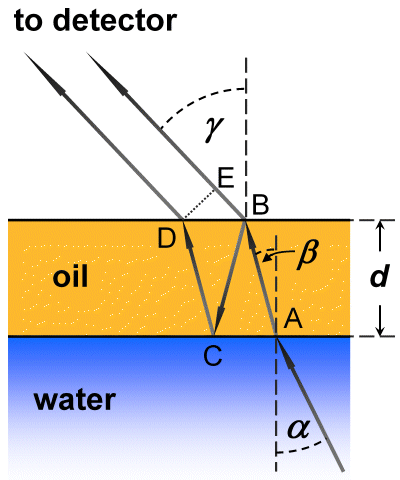
We want to get a deeper understanding of the interference fringes observed with microwave radiometry. In the graph, the geometric difference of the path of rays Δs of the waves is: $\Delta s=n_{oil}\left(\overline{BC}+\overline{CD}\right)-\overline{BE}$ Using trigonometric relations and Snell’s Law, this becomes: $\Delta s=2d\sqrt{n_{oil}^2-{sin}^2\gamma }$ Due to this geometric path difference, there is a phase difference $\Delta \varphi$ of the waves: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s$ At point C, the wave undergoes a reflection at a medium with higher refractive index (i.e., the water). Hence, there is a phase jump of π of the reflected wave. The phase difference of the waves becomes: $\Delta \varphi =\frac{2\pi }{\lambda }\Delta s-\pi$ where the term -π is from the phase jump at point C. There is constructive interference with $\Delta \varphi =\pi m$ and destructive interference with $\Delta \varphi =\pi (2m+1)$, where m is an integer number.

An oil layer with thickness d on the water surface, and microwaves with a path of rays directed towards the detector of the microwave radiometer.

Exercises

Continued from Worksheet Marine Pollution C02-02-3):

7. Using trigonometric relations and Snell’s Law, show that the geometric path difference Δs of the waves holds as given above, depending on the oil layer thickness d, the refractive index n of the oil, and the incidence angle α.
8. Please calculate the phase difference of waves for an oil layer thickness from 0 to 5 mm in steps of 0.25 mm with the following data: f=34 GHz, n_oil=1.41, γ=50°. Take also into account the phase jump of the wave reflected at point C. Verify the correctness of the position of maxima and minima of the brightness temperature curve shown on page 2 of the supplement on Microwave Radiometers.

Materials

• Version of this supplement worksheet: Interference fringes of oil on water, as printable rtf file
• Oil pollution and the fate of oil at sea
• Airborne maritime oil spill surveillance
• The Microwave Radiometer

Background Information

• Textbooks on optics; the topic is identical with the interference of light waves that are transmitted through (or: reflected by) a thin plane parallel glass plate.