Supplement 7.3: Raman Scattering (5/6)

Raman scattering of water

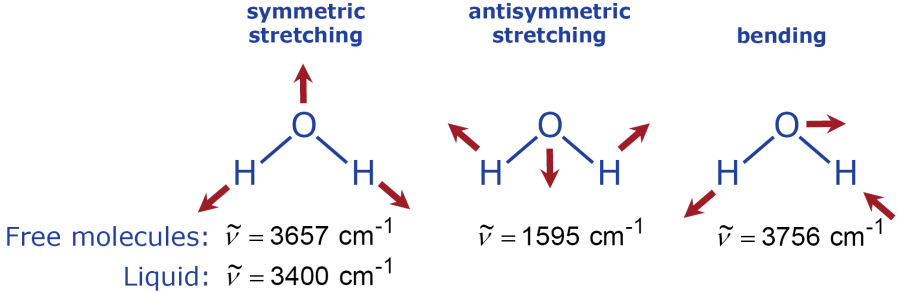
Now we can express the three vibrational modes of the water molecule (shown on page 3 of this supplement) not only as frequencies f but also in wavenumbers $\tilde{\nu }$.

The three vibrational modes of a water molecule with their wavenumbers.

Unlike the Raman lines of water in the gas phase, the Raman lines of liquid water are spectrally broad. This is due to molecular collisions in the liquid that cause perturbations of the energy states. Such lines are called Raman bands. Based on the energy balance equation of the Stokes shifted Raman bands (see diagram on right column of previous page)

we derive by using $c=f\lambda$ und $\Delta E=hc\tilde{\nu }$ the relationship

where ${\lambda }_1$ is the wavelength of the absorbed light and ${\lambda }_2$ ed is the wavelength of the Stokes shift Raman band. ${\lambda }_1$ refers to the excitation wavelength and ${\lambda }_2$ refers to the Raman wavelength.

The following diagram illustrates the Raman wavelengths of liquid water with three different excitation wavelengths.

Spectra of the intensity of three Raman bands of liquid water, each being excited at wavelengths as indicated by blue arrows: 400 nm (violet), 475 nm (blue) and 500 nm (blue-green). The red arrows indicate the Stokes shift of the Raman emission wavelengths.

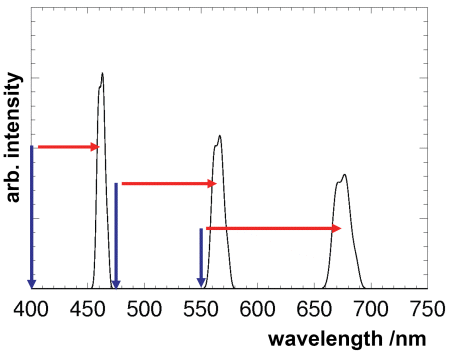
The diagram shows clearly that the difference of the Raman wavelength to the excitation wavelength does not remain constant all throughout, but rather increases with increasing excitation wavelength. It is evident from the energy balance equation, that it is not the wavelength difference but rather the energy difference $\Delta E$ or rather $\tilde{\nu }$ which is invariant.